Modeling¶

Use of this tool
This tool is : advanced; complicated; challenging to use – but really powerful
The use of this tool is recommended to everyone who is trying to model small angle scattering from complicated system which requires combination of different models. It is challenging, but it is very capable.
Features
Multiple input data sets at the same time. Up to 10 input data sets can be loaded at the same time and fitting/modeling can be done to one or more data sets at any time.
Up to 10 populations of scatterers can be combined. Any population can be arbitrarily “switched on and off”. Any population also can be one of : “Size distribution”, “Unified level”, “Surface fractal”, “Mass Fractal”, or “Diffraction peak”; allowing to model really complex small-angle scattering data.
Each population can have different contrast for each data set. Note, that this means up to 100 contrasts, potentially.
Form factor parameters can be fitted. That does not mean the data must allow them to be fitted, but the tool will allow any form factor parameter to be fitted.
Structure Factors – library of 5 structure factors to be used. See Structure factor description in the “Form factor and Structure factor description” pdf file.
Optimized for speed - much faster fitting when “semi-auto” R distribution is selected for complicated form factors.
Input of “model” data when no real data are loaded, but only q-data are created to model SAS from microstructure without the need for measured data.
Logging during use of this tool – This tool similarly to other Irena tools logs state of the parameters before and after each fitting. The purpose is to enable at least some recovery, if fitting goes to never-never land and user accidentally looses the “recovery” option by using revert fit (by hitting the fit button second time etc…). The notebook can be pulled up by using menu SAS -> Other tools -> Show SAS Logbook. This logbook is mess of information, but all necessary information to recover should be there. It is not formatted in any particularly meaningful way, though. As output use the “Save in notebook” option discussed later in this chapter.
Theory behind this tool¶
Modeling II can use up to 10 “populations” or models : each can be either “Size Distribution of scatterers”, “Unified level”, “Surface Fractal”, “Mass Fractal”, or “Diffraction peak”; For the Size distribution and Unified level the SAS from them can be calculated in dilute limit or after applying one of 5 available structure factors.
NOTE: “Unified level” : this is kind of simplified Unified level and the tool will complain (once every 24 hours) if you try to use more than one Unified level. It is not impossible, but it is discouraged. If you need more Unified levels, you need “Unified fit” tool. There are various rules and relationships, which can be enforced in that tool. The reason for Unified level here is to enable one combine scattering from particulate system with the scattering from fractal system formed by these particles. Typical use is to describe low-q power law slope, which is mass fractal of primary particles, which then can be modeled correctly. For more details, read: Unified Fit.
NOTE: “Diffraction peak” : this is simplified version of Diffraction tool and for now there is no way to include relationships between the peaks (to provide for specific structures) as the Diffraction tool allows. Fort more details on the terms, peak profiles etc. read the Diffraction tool chapter.
NOTE: “Mass Fractal” and “Surface Fractal” : These are analytical formulas of mass fractal and surface fractal. The use and parameters copy dedicated tool Fractal model For details see also Mass and Surface Fractals.
NOTE: “Size distribution models” : the tool is aware of the units of Intensity (either in the wave note or set by user) and its GUI is changing depending on these units. What was originally called “Volume” of scatterers for size distribution is now:
“Scale” if data are on arbitrary scale. This value has no direct physical meaning, except it may be relative measure of volume between samples if the data are properly normalized.
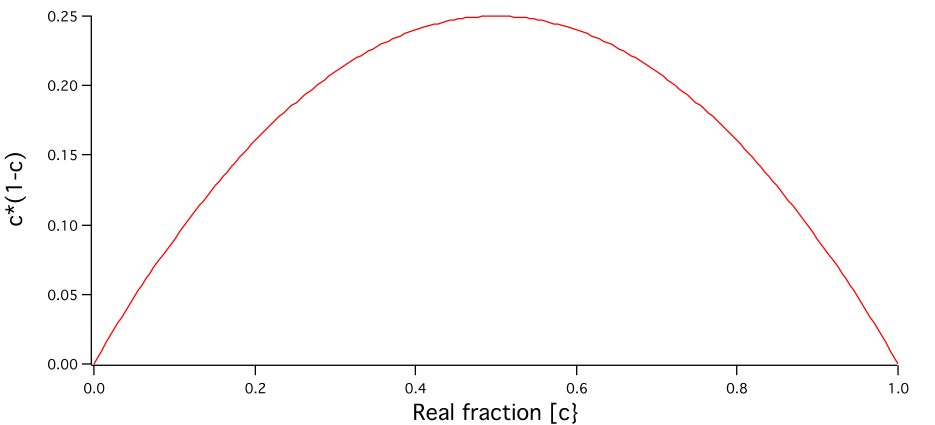
“Fraction” if data are on cm2/cm3 scale. This is what originally was “Volume” as this were the default “units” the tool assumed. However, note this is what in the dilute limit we call volume fraction c, but for higher volume fractions this approximation (made commonly!) is wrong, in calculations this represents really c(1-c)!!! If you get this value >0.25 something is really wrong here and you do not have physically meaningful model or correct data. This Fraction should never get higher than 0.25, see graph below:
“Volume [cm3/g]” if data are on cm2/g scale. This is if the SAS data are calibrated per gram of sample.
What is size distribution
The size distribution is modeled as small angle scattering (SAS) using basic SAS formula:
where \(\Delta \rho\) is contrast, F(Q,r) is scattering form factor, V(r) is the particle volume, N is the total number of scattering particles, P(r) is the probability of occurrence of scatterer at size of r. This formula is, of course, replaced by summation formula with limited number of bins in radii. Therefore the formula coded in is following:
This formula has been coded very many times… Following are comments, which address specific parts of this formula.
Three different distribution models are available – Gauss (Normal), Log-Normal, and LSW (Lifshitz-Slyozov-Wagner used in precipitation theory involving Ostwald Ripening).
Irena uses by default automatic selection of radia distribution – ranges needed, bin widths etc. – with user selectable precision and number of steps. For details see Irena manuscript which goes to details on this subject. Alternatively, user can select to provide radii distribution definition parameters manually and therefore generate distribution of his/her choosing. Default automatic method is likely the best for very large fraction of users.
Number of form and structure factors are available. Note, that it is relatively easy to add other shapes in the code, so if anyone needs (really needs) another shape, let me know… Calculation speed of different form factors varies significantly depending on calculations needed to calculate involved integrals.
Structure factors
The code includes number of Structure factors to account for interaction among the particles for non-dilute systems, which can be independently switched on or off for each population of the scatterers. User should be aware of the crudeness of any of these calculations.
The code used for calculations involves correcting intensity from a population of scatterers using this formula:
Intensitywith interference(Q, R) =Intensitywithout interference (Q,R) * Structure factor (Q,R)
Description and details on the structure factors are in the Igor help file or pdf file “Form and Structure description” which can be opened from the Irena menu.
Remember: these method accounts in very crude way ONLY for interaction for particles in the particular population. If there are interactions among particles from different populations – which is very likely – these calculations have NO WAY to account for it.
Important Information The code uses for all size related parameters Angstroms (10-10 m) or for Q vector (A-1). In the case of scattering contrast, number distribution and any other volume contents centimeters (10-2 m). This code uses either Diameter or Radii for scatterer size.
Distributions \(\Psi (r)\) and \(V(r) \Psi (r)\) and distribution of r.
The code can work with distributions defined as number distribution \(N * \Psi (r)\), where integral over \(\Psi (r)\) for all r is 1 and N is total number of scatterers or for volume distribution \(V_{tot} * \Psi (r)\), where integral over this term is equal total volume of scatterers. Internally, the code actually always works with number distributions \(N * \Psi (r)\), which, in the second case is calculated from the total volume of scatterers.
There are currently 4 different distributions built in the code, which can be used independently for any of up to 5 scatterers populations: Gauss (normal), Log-Normal, LSW, and Ardell.
Gauss and Log-Normal distribution definitions were adopted from NIST engineering statistics handbook. See http://www.itl.nist.gov/div898/handbook/eda/section3/eda366.htm
Standard complicated log-normal distribution is defined as follows (Allen, A.J., Krueger, S., Skandan, G., Long, G.G., Hahn, H., Kerch, H.M., Parker, J.C. and Ali, M.N. (1996). J. Am. Ceram. Soc. 79, 1201-1212., Filliben, J.J. (2006). Exploratory Data Analysis, in NIST/SEMATECH e-Handbook of Statistical Methods, edited by C. Croarkin and P. Tobias, p. 1.3.6.6.9, available online at http://www.itl.nist.gov/div898/handbook/. Gaithersburg, MD: NIST.):
The NIST definition is modified to be more elegant and parameters used by Irena package are as follows:
“Min” = Dmin
“Mean” = (Dmed - Dmin)
“Sdev” = sigma = ln((Dmed-Dmin)/(Dmode-Dmin))
The LSW distribution has been accepted from a source by J. Nasser, A. K. Kuruvilla, and J. E. Smith Jr. These authors in their manuscript on the web (www.space.gc.ca/science/space_science/paper_reports/spacebound97/materials_sciece/….) refer to distribution by Lifshitz, Slyozlov, and Wagner:
This is the particle size distribution predicted by LSW in their theory of Ostwald Ripening.
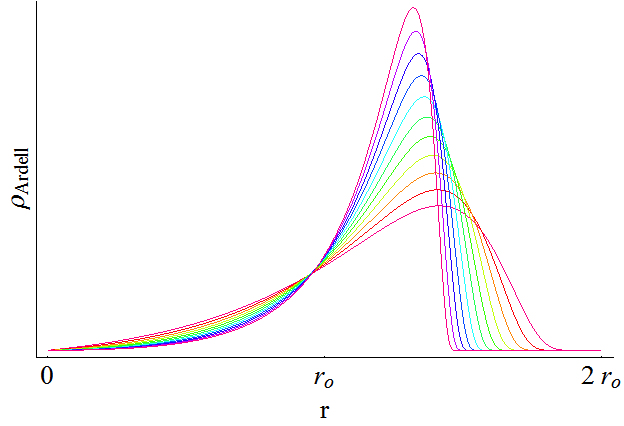
Ardell distribution has been adopted per request (by our metallurgy colleagues) based on papers: Ardell, AJ and Ozolins, V., Trans-interface diffusion-controlled coarsening, Nature Materials, Vol. 4, pg. 309, April 2005 and Ardell, A.J., Quantitative predictions of the trans-interface diffusion-controlled theory of particle coarsening, Acta materialia 58 (2010), 4325-4331. Here are the formulas for the distribution:
where n is between 2 and 3, resulting in this distribution as function of n:
Automatic radii distribution Each distribution in this type of problems needs an appropriate selection of radial bins. Appropriate selection is actually problem – too many bins cause too long calculation times, narrow range of radii causes some significant volume of scatterers to be neglected, etc. In this code I take a different approach, which is important to explain properly:
For each distribution I create cumulative distribution (if exists using formula, if not numerically). Using user input value I select range of radii in which the value for cumulative distribution is between this value and (1-this value). This causes, that only the tails, for which the cumulative probability is below the user selected value are neglected, giving user full control of the precision in which we/she wants to model the data. Then radial bins are calculated, so their spacing for cumulative probability is the same. This causes that the bins have varying width – are narrowest around the areas, where probability function changes fast and wider in the tails. This should provide the best possible method for using the binning method, I hope… All of the code handles bins of varying width…
F(Q,r) problem – applicable ONLY to integrated spheroid
For the case of integrated spheroids ONLY - rarely addressed problem is related to usual method of calculation of F(Q,r), independent of selected particle shape. In usual method of modeling – using bins this problem is usually neglected. Standard method is to take for radius the center point of the bin, and calculate F(Q,r) for this point. However, this may be very incorrect - the F(Q,r) is a strong function of Q*r (with period of pi). Through the Q range and size range studied, the number of periods in pi within the bin width * Q varies strongly. Taking just center of the bin for calculating F(Q,r) results in nearly random selection of the r for this calculation and can result in significant error. Calculated value may be very far from average F(Q,r) value, which we should properly used. *In case of data from USAXS instrument we at least have no problem with definition of Q – the Q resolution is very high, otherwise we would have to worry about the Q variation within the Q point - smearing
Anyway, to avoid problems with the oscillatory behavior of the F(Qr) the code takes at least 3 – and maximum 61 F(Qr) values within the bin in radius (at least start, middle and end of the radius bin point), linearly distributed in the bin, multiply them by appropriate V(r) and then average the result. The number of points within the bin is obtained as floor(3+abs((10*(QRMax-QRMin)/pi))), with maximum being 61.
This causes significant increase in the calculation time… Keep this in mind.
— end of part valid ONLY for spheroids
The above does not apply for other shapes – globs by definition do not exhibit this problem and I have not included this complication for other shapes. The standard spheroids also do not have this included – if you want to use this integration method, use even for spheres “integrated spheroid” and aspect ratio 1.
SINGLE input data set - size distribution¶
This subchapter relates ONLY to Size distribution type of “population” in Modeling II. Please, use this to learn about the specific related to size distribution use and the types of parameters. Next chapter will describe use of Unified fit and Diffraction peaks. It is not easy to find nice case example data to produce one chapter together. Also, it may be really confusing to mix and match these models. Start tool from SAS menu, it is titled “Modeling II”.
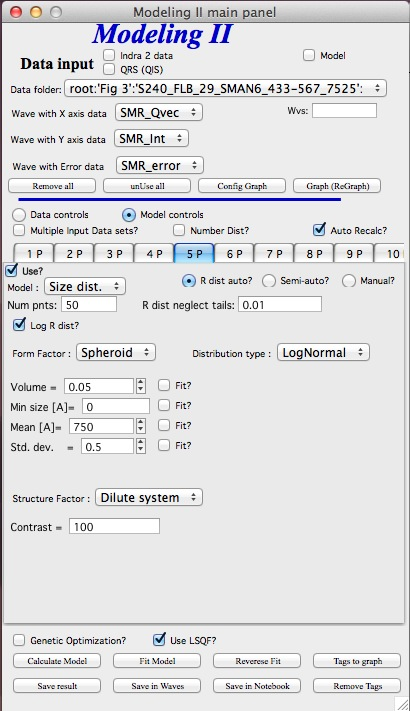
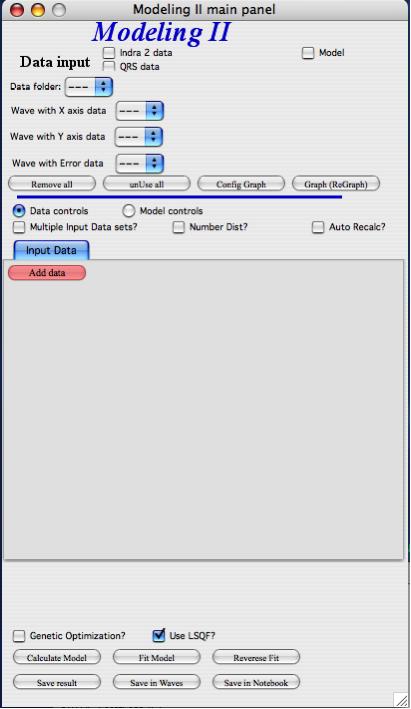
GUI description
In the top part are standard data selection tools, this package can also be scripted by scripting tool. Note in following image, that the tool has somehow different GUI. The lower 2/3 of panel change depending on selection of radio-buttons “Data controls” and “Model controls”. See image below. Also, if only one data set will be used, make sure the checkbox below “Data controls” is unchecked (only one tab “Input Data” is visible). Note, that there are few buttons just under the Data input popup controls: “Remove all”, “unUseAll” “Config Graph” and “Graph(reGraph)”. These are tools to control global behavior or resent the tool.
“Remove all” button removes all input data from the tool.
“unUseAll” button sets all of the input data sets to not to be used. (useful only with multiple data input)
“Config Graph” opens control screen for graph controls (font size etc.). These values are common for all tools (once I propagate them through whole package).
“Graph (reGraph)” button creates the graph or forces redraw of the graph.
Note one more checkbox which is worth mentioning here… It is little bit lower, on the right hand side and is called “Auto recalc?”. If checked the model will be recalculated with every change of any parameter (except Form factor parameters, which cannot trigger this). Use only on fast computers and simple enough model, or it can be tedious.
“More parameters” button opens another panel with choices of Intensity units (if need to be set manually), choice if size for size distributions is diameters of radii (default radii), and if the size distribution is Number distribution of Volume distribution.
NOTE: In version 2.62 I have added ability to make smaller steps for the parameters of the models, when changed by clicking on the little arrows up/down on the right hand size of the field. By default when you click the arrow a new step is set for next click, which is about 5% of the current value. This makes sure what one can make sensibly large step for any value. But 5% may be sometimes too much and so I added ability to hold down modifier key – any one of ctrl/cmd/alt/shift. If you hold the modifier down and click on the arrow, next step will be set to 0.5%. Note, that the first step is still large, but following will be small, and if a modifier key is held down during clicking, you will be making small steps. Should be valid for all Model parameters (size distribution/peak, unified fit/…).
Data controls
The data available in the test.pxp file distributed with the Irena package are in qrs structure, so select “QRS data” and pick the ‘Test data”. To load data into the tool use the red button “Add data” on the left top corner of the Input Data tab.
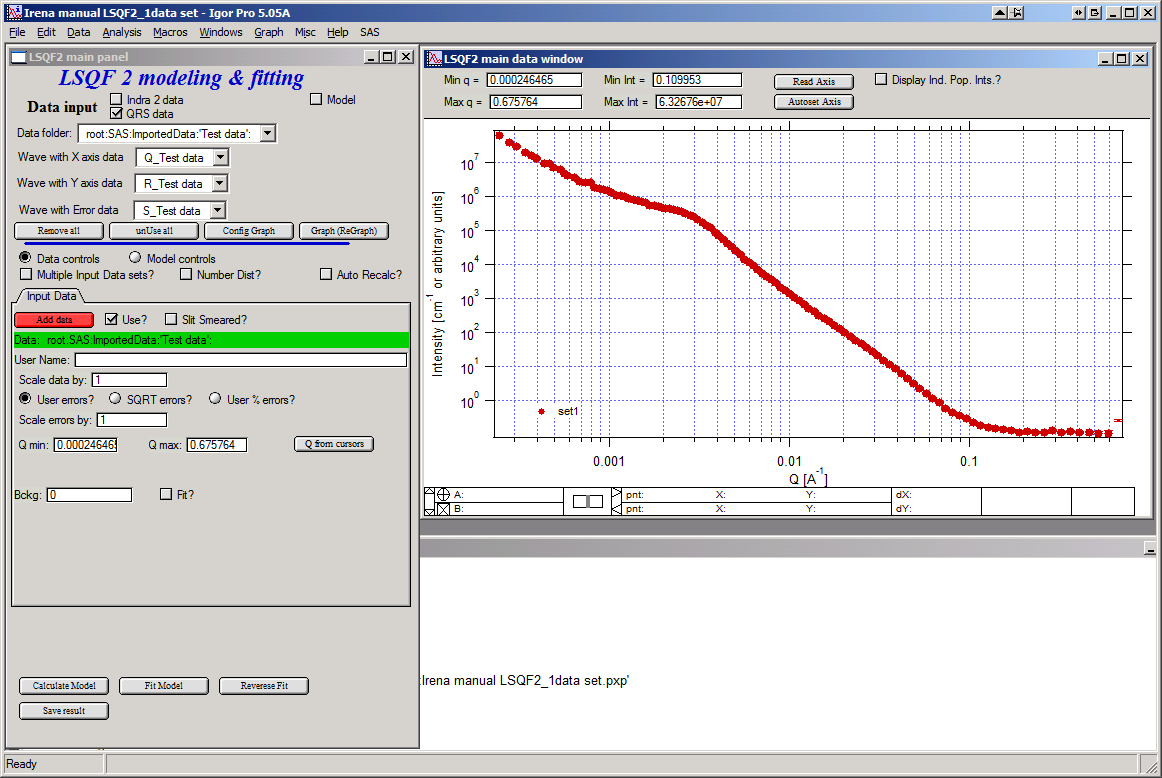
Description of parameters on the Input data tab:
Checkbox “Use?” allows to select if this data set is used in the tool. This is really useful when multiple data sets are used.
Checkbox “Slit/Q resolution smeared” if slit smeared data are used - or if you want to account for Q smearing, select. New panel will appear. If you close this panel and need to reopen it, just uncheck and check the checkbox again.
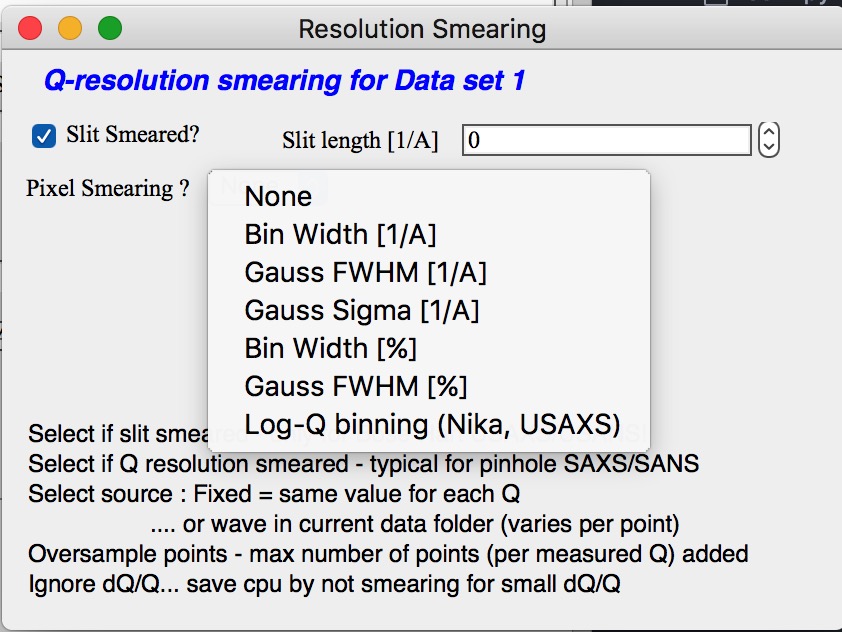
Number of various Q resolutions is now included. They are described on the panel in some detail. Note, that it is possible to have data which are both Slit smeared data AND at the same time require Pixel/Q smearing - for example from my APS USAXS instrument.
More controls appear on this screen if necessary to guide you to provide correct values. These values may be calculated when appropriate or can be provided to Modeling as wave of values, in the QRS naming system the wave name starts with w_. Proper Q/pixel smearing can be challenge and its hadnling mathematially requires singificant amount of CPU power, so it is worth while to evaluate, if it is really necessary to deal with. For highly polydiperse systems on most X-ray instruments Q resolution is NOT necessary to consider. For monodispersed systems and/or SANS instruments it may be appropriate to address this. If you need more guidance, talk to me…
“Data” field. This field contains path to data within Igor experiment. Cannot be edited.
“User name” user editable name for the data. Will be used in the graph – needed to make sense in case of use of multiple input data. If empty, default name will be used (not very informative).
“Scale data by” field – user can scale data here. For example some data may need to recalibrated, converted to 1/cm or whatever. Ideally should not need to be used.
Radio buttons “User errors”, “SQRT errors”, and “User % errors” – what type of errors to use for this particular data set? User errors are provided by wave with error data, SQRt errors are square root of intensity and when % error is used, the error is set to 1 % of intensity.
Scale errors by:” allows scaling errors by factor. Errors are produced using method selected above and then scaled by the factor user provides here.
“Qmin” and “Qmax” – selection on fitting interval of data – can be typed in or using the button “Q from cursors” can be read from cursor position. Only data within this interval will be used for fitting.
“Bckg” Background for this data set. Can be fitted (“Fit?” checkbox will open fields for Min and Max limits for fitting… Further controls are likely going to appear…
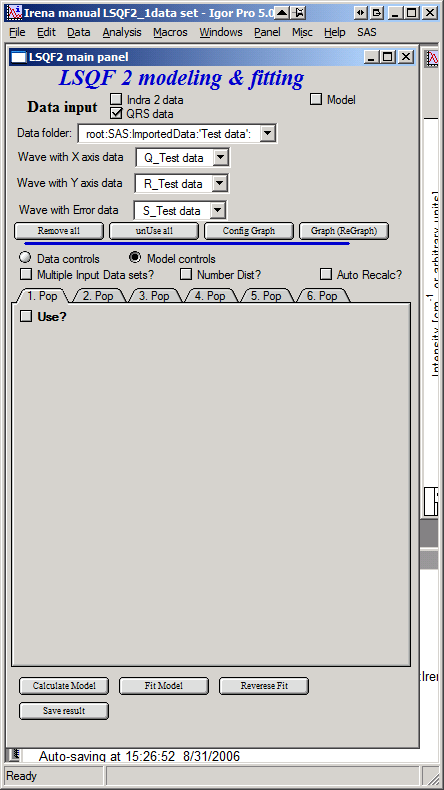
Model controls
Model controls become available by selecting “Model controls” radio button above the tabs.
Note the checkbox “Number Dist?” – if checked the distribution will be considered to be number distribution, if unchecked (default) the distribution is volume distribution.
Controls for any population appear when “Use?” checkbox is selected… see below:
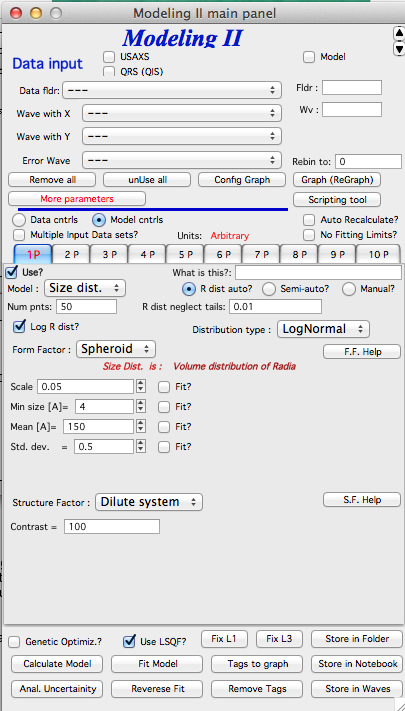
Description of controls:
“Model :” Select what model to use for this population. “Size dist.” chooses size distribution, other options are “Unified Level”, “Surface Fractal”, “Mass Fractal”, or “Diffraction peak”. These are described in subsequent chapter.
“What is this :” User string for naming that population. Something like: “BC precipitates”, “voids”,… Something useful for plotting purposes as it was simply getting too difficult to navigate through with only population number.
“R dist auto?” distribution of radii selected automatically for given distribution. As in the older LSQF (chapter 9) the R distribution here is selected in such way, that densest points in R are at the middle of the distribution (around maximum) and then they spread with large and larger steps.
“R dist semi-auto” same as above, except the R distribution is not being changed during fitting. Therefore one needs to be close to final solution when starting fitting. But this way the fitting can be MUCH faster for complicated form factors. Since the R points and q-points do not change during fitting, G matrix (which is cashed internally for each population and data set) is calculated ONLY once. Major time saver…
“R dist manual?” Manually input min/max R for each distribution. Opens control fields needed for input.
“Num pnts” Number of points in R distribution. Use sensible numbers. Large numbers will take a lot of time.
“R dist neglect tails” same meaning as in LSQF (chapter 9). Basically what fraction of volume of size distribution can be neglected. Allows truncation at small/large sizes - defines Rmin and Rmax for automatic/semi-automatic R distribution method.
“Log R dist?” – select to have R points logarithmically distributed. If unchecked, linearly distributed bins in R will be created.
“Form Factor” – select form factor from list of available form factors. May open another control screen for parameters of the form factors. To get this controls screen again, re-select the form factor and the screen will pop up.
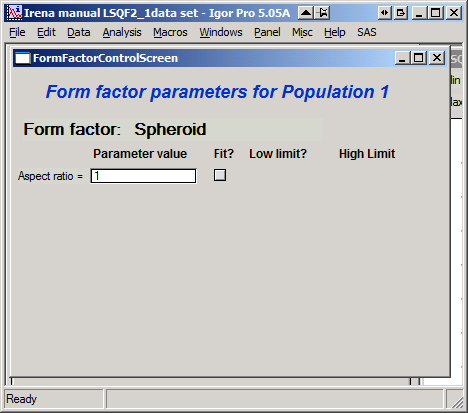
This is example of screen for Spheroid. Note, that there is one parameter for this Form factor (aspect ratio). This parameter can be fitted in this tool. By selecting “Fit?” checkbox, low an high limits fields will appear.
“Distribution type” select “lognormal”, “Gauss” or “LSW”. Definitions are in LSQF (chapter 9). Parameters for these distributions are now separate, so one can go among them and the parameters will not be reused/lost from previous use of that particular distribution type…
“Volume” – volume of scatterers in this population. “Fit?” checkbox allows fitting. Fields for min/maxc values will appear. When volume is changed manually by typing in this field, min and max are automatically set to 1/5 and 5x the typed value. Therefore, it is important to first set the value and then, if necessary change the limits. Not the other way around!!! LogNormal parameters
See details in the chapter 9.3 for details… Formula:
“Min size”, “Mean” , “Std Dev.”
Gauss
Has just two parameters: “Mean size” and “Width”.
LSW
Just one parameter: “Position”. For details see chapter 9.3.
Schulz-Zimm
Schulz-Zimm distribution was added by modifying code from Scatter 3, see reference: Stephan Furster and Christian Burger, Scattering Functions of Polymeric Core-Shell Structures and Excluded Volume Chains, Macromolecules 1998, 31 (879-881). Here is the code. Irena presents user with parameters *width* and *MeanPos*:
b = 1/(*width*/(2**MeanPos*))^2
a = b / *MeanPos*
if(b<70)
y=( (a^(b+1))/gamma(b+1) * x^b / exp(a*x) )
else //do it in logs to avoid large numbers
y=exp( (b+1)*ln(a)- gammln(b+1) + B*ln(x) - (a*x) )
endif
“Structure factor” Popup allows selection of one of included structure factors (see pdf file with description). The structure factors have their own screens and parameters can be fitted. See below for case example:
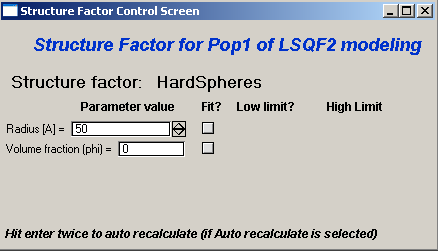
Note, that due to quirk in Igor way of controlling updates you need to hit enter twice to automatically recalculate the curve (when checkbox on main panel is selected)…
“Contrast” field – input contrast. Only one contrast in case of single input data set.
Last few buttons
Under the tab area there are few more control buttons.
“Calculate model” calculates Intensity for current model.
“Fit model” Runs fitting with currently selected parameters to fit.
“Reverse fit” recover parameters stored before the current fit run.
“Save result” Saves result into the folder. It feature is not fully finished yet. This is difficult to know what is expected in case of multiple data input…
“Save in Waves” Saves results into new folder in form meant for creating tables with results. In this case new folder (user is presented with dialog to create new name) is created and for each internal variable/string is created new wave. This creates large number of waves – most useless… But user then can create table of selected waves with important results – for example sample name, volume of pop1, mean diameter of pop1 etc.
“Save in notebook” Creates Igor Notebook (formatted) and pastes in this notebook summary of current state of the tool in more or less human readable form. This includes copy of the graphs and somehow reasonably formatted listing of parameters.
Comment: If user decides to do NOLY modeling with no real input data - by using “model” checkbox when adding data in the tool – there is no real “output” place where to put the modeled data for future use. Starting from release 2.41 dialog is presented to user and user can input name of new folder, which will be created, and the model data will be saved there.
“Unified level”, “Surface Fractal”, “Mass Fractal”, and “Diffraction peak”¶
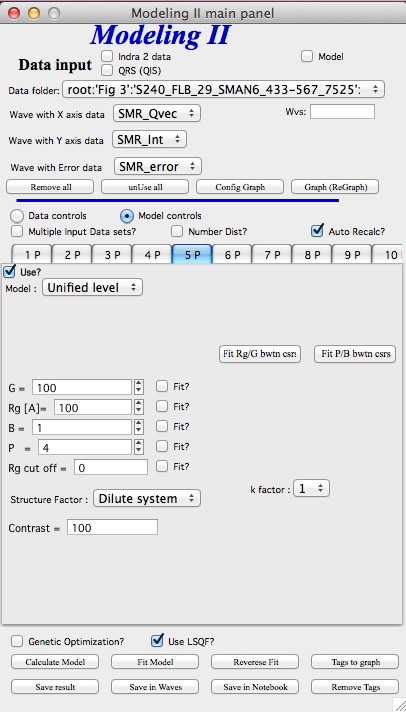
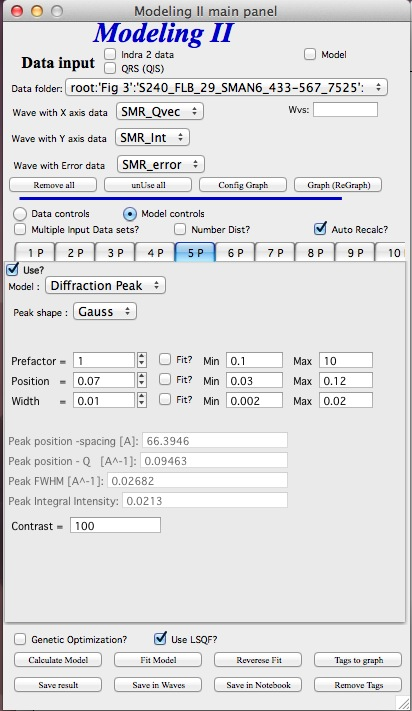
Select Model: “Unified level”, “Surface Fractal”, “Mass Fractal”, or “Diffraction peak”. Note, that different controls appear in the panel.
NOTE:
These implementations of “Unified level” and “Diffraction peak” have contrast in it, so Unified parameters G and B and Diffraction peak parameter “Prefactor” are multiplied by contrast when used in calculations. This is different from Unified fit and Small-angle Diffraction tools, which do not know about any contrasts. This is important for modeling of data where user has multiple input data sets and each has different contrast for the population represented by the Unified level. Such as Anomalous data or combined X-ray and neutron data etc. Be aware, that B, G, and Prefactor will be different for modeling by Modeling II and Unified fit or Small-angle Diffraction tools. Also, note, that the Unified fit data analysis tools DO NOT work with Unified fit results from Modeling II.
Note also, that “Peak Intg. intensity” in “Diffraction peak” model is calculated WITHOUT contrast included.
While the choices above are open for discussion, logically these are the only and right choice as for fitting for multiple data sets only one G, B, and “Peak Intg. Intensity” can be calculated.
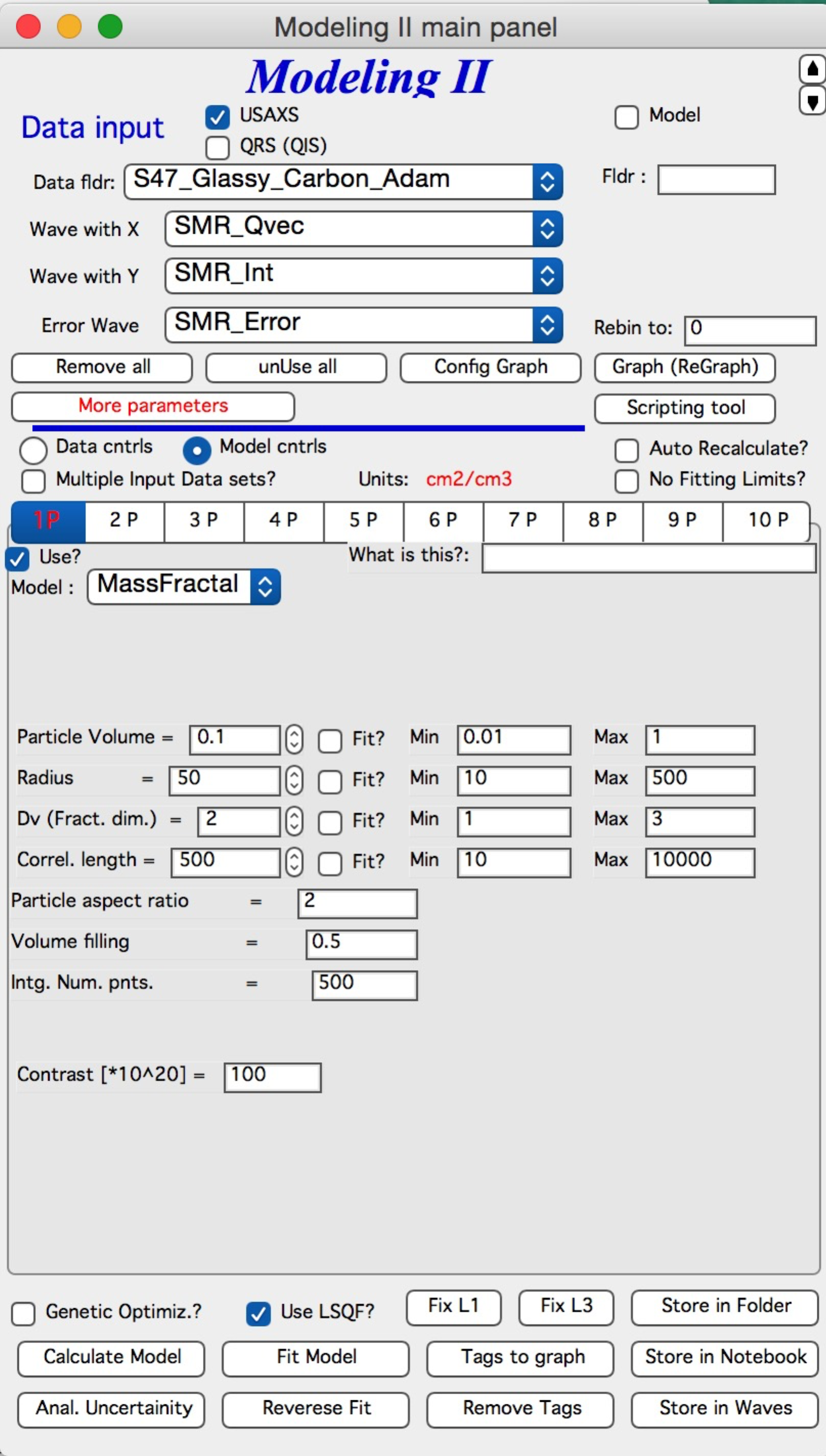

NOTE: for real details on the parameters used in the Fractals panels (above), please refer to the chapter on Fractals tool. It really makes no sense to reproduce it twice in the same manual. ****************************
Here is fitting example when complicated data set is fitted with two Unified levels and two peaks. This is complicated system and data are not attached. Also, these data are slit smeared so the fitting is bit more complicated. This case is used mainly as example of GUI and tool capabilities.
Bellow are data, the data were identified to be composed of two types of components :
Low Q scattering of some size distribution of highly asymmetric particles with two Guinier areas ~ 0.0003 and 0.004 A-1 connected by power law slope. This system may be fit-able by size distribution but it was found easier to fit by two-levels Unified fit.
Two diffraction peaks Q ~ 0.025 and 0.07 A-1
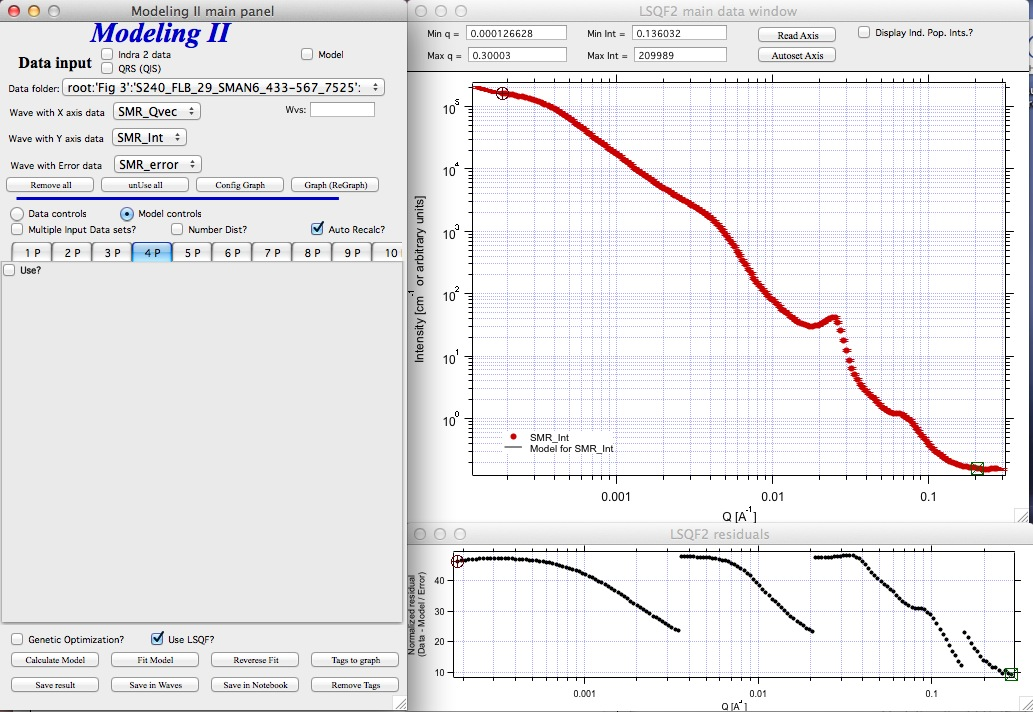
Unified fit with two levels
Selecting in 1P Model as “Unified level” we get appropriate controls:

Next we can select with cursors the are where Guinier dominates in graph and use button “Fit Rg/G btwn csrs” to fit Rg and G: Here is the result:

Note the blue curve that is the Guiner fit to the data. Next we select power law area at higher Q and fit the P/B:
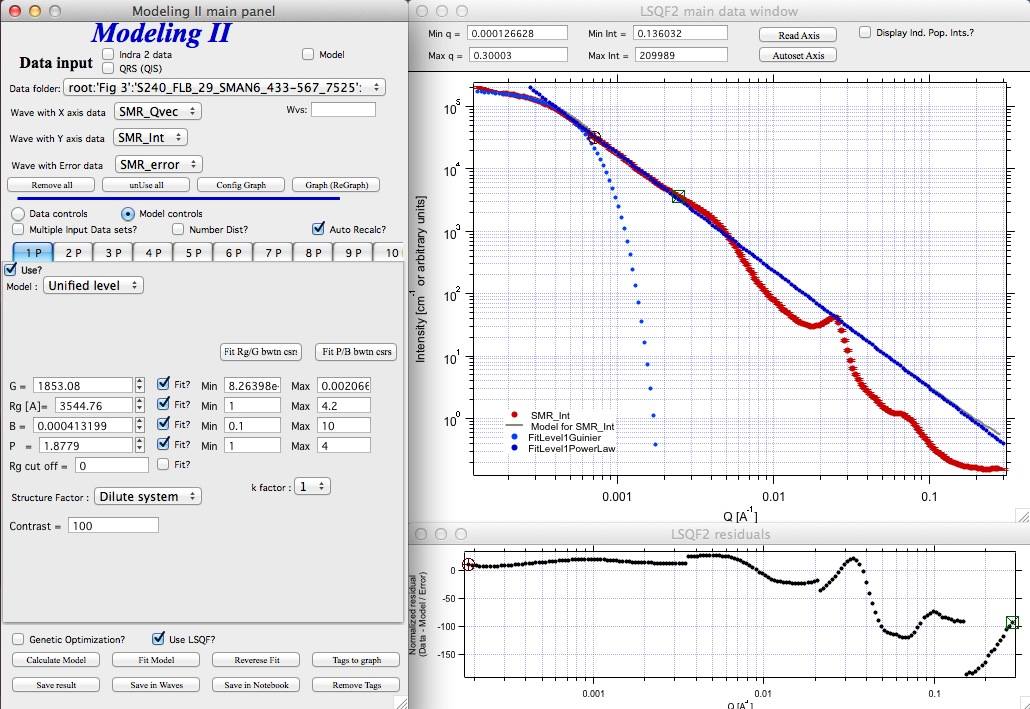
Note that the slope P is close to 2 so this looks like plane-like object and that the scattering needs to be terminated at Rg of the next (smaller) Guinier area. Select 2P as Unified level and fit the Guinier area there also:

The Rg of the 2P is about 467A, so we can now transfer this number to RgCO of the 1P and then we can also fit the B/P to higher Q values power law slope:
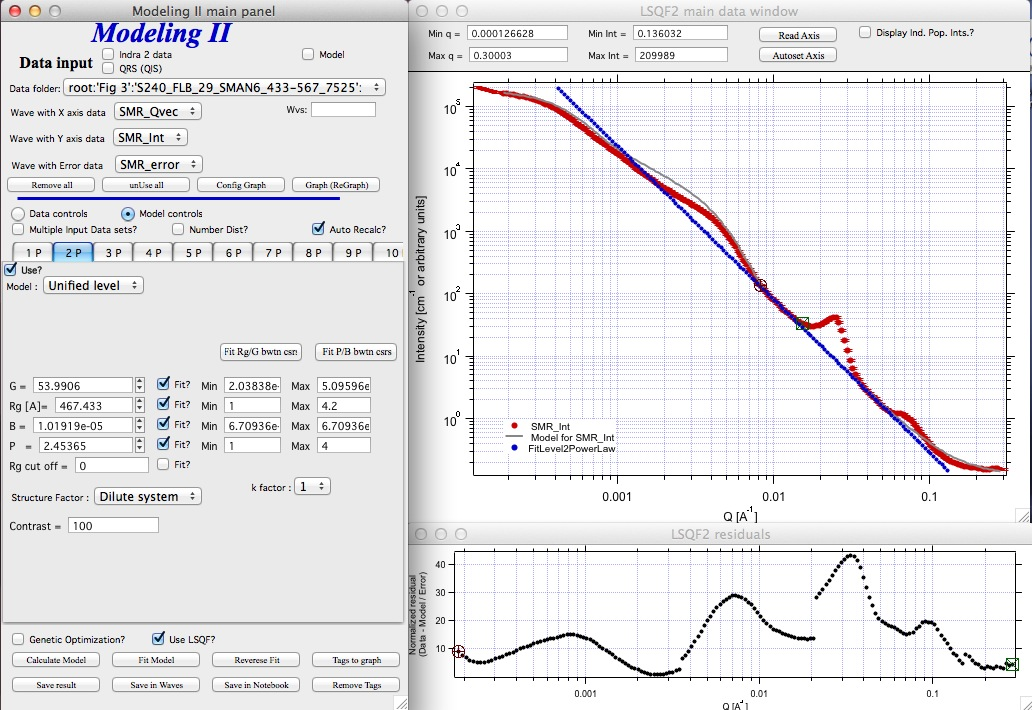
Note, that on the “Data controls” set of tabs in the “Data 1” tab I have already set the background to about 0.12 and also checked “Fit?” checkbox there.
Next we need to add the diffraction peaks, 3P will be the first peak:
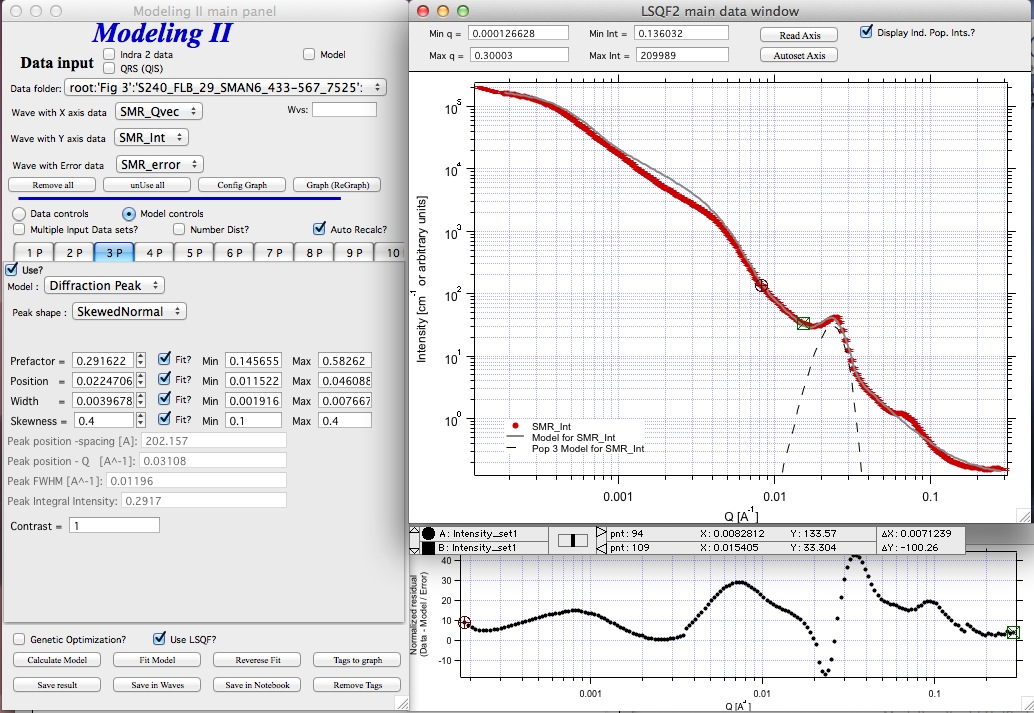
Note, I have played with these data already and found “SkewedNormal” shape to be the best. I checked here the “Display Ind. Pop. Ints?” at the top of the main graph here as that helps for you to see the peak.
And next we will set the 4P as diffraction peak:
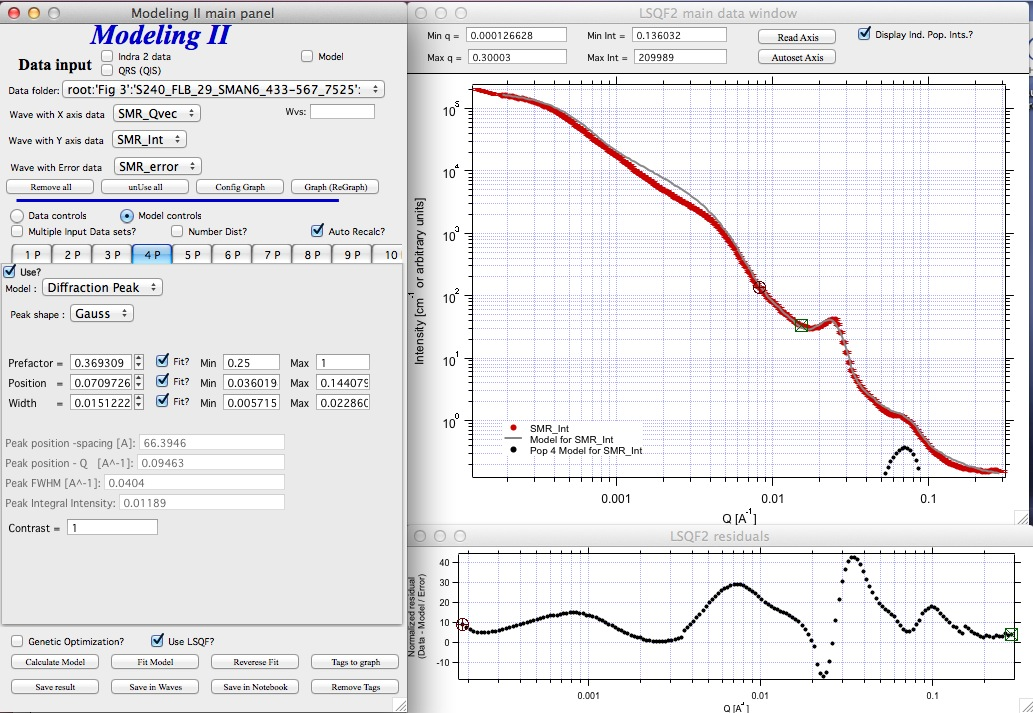
Note the changes in the bottom window, which displays “normalized residuals”.
Next we can fit the parameters and then push the “Tags to graph” button
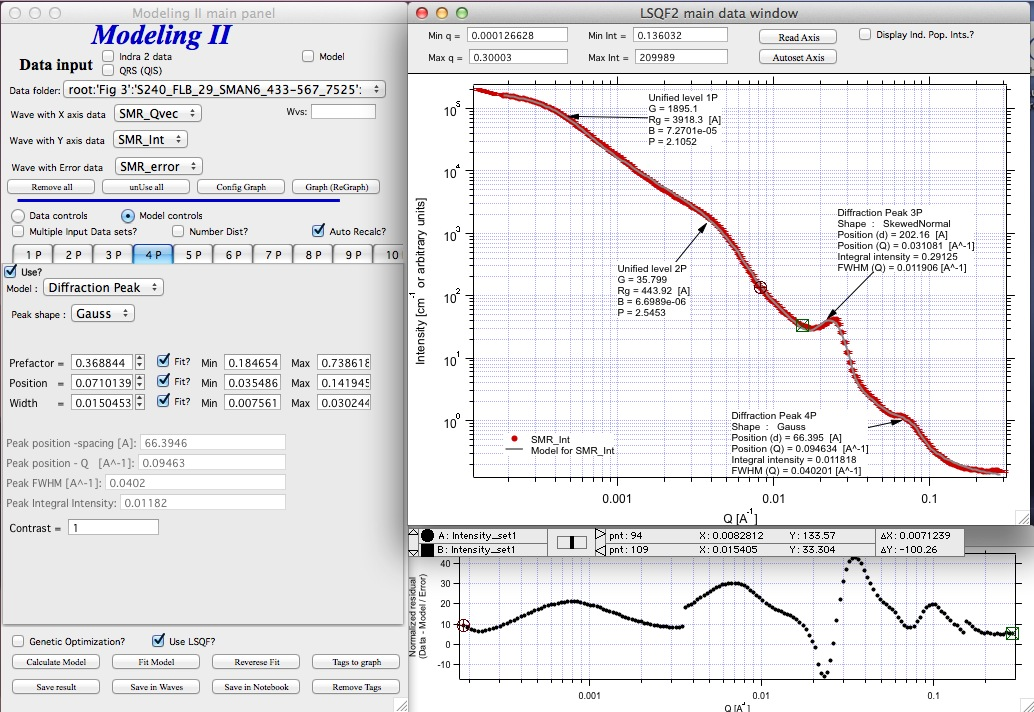
This is the best result with this model I was able to get.
You can also now store the results in Notebook for export to Word processor or as record of your results. Of course you should save your results in folder with “Save results”.
Here is the Notebook record of these results
************************************************
Results saved on Fri, Dec 30, 2011 4:24:57 PM Single data set used: FolderName_set1 = root:’Fig 3’:’S240_FLB_29_SMAN6_433-567_7525’: IntensityDataName_set1 = SMR_Int QvecDataName_set1 = SMR_Qvec ErrorDataName_set1 = SMR_error UserDataSetName_set1 = SMR_Int DataScalingFactor_set1 = 1 ErrorScalingFactor_set1 = 1 Qmin_set1 = 0.00018493 Qmax_set1 = 0.28792 Background_set1 = 0.11996

LSQF2 main data window

Normalized residuals

Size distributions
Model data for 4 population(s) used to obtain above results Summary results for population 1 This population was Unified level Contrast = 100 Unified level Rg = 3918.3 Unified level G = 1895.1 Unified level B = 7.2701e-05 Unified level P = 2.1052 Unified level RGCo = 467 Unified level K = 1 Structure factor description and parameters StructureFactor = Dilute system
Summary results for population 2 This population was Unified level Contrast = 100 Unified level Rg = 443.92 Unified level G = 35.799 Unified level B = 6.6989e-06 Unified level P = 2.5453 Unified level RGCo = 0 Unified level K = 1 Structure factor description and parameters StructureFactor = Dilute system
Summary results for population 3 This population was Diffraction Peak Contrast = 1 Peak profile shape = SkewedNormal Peak D position [A] = 202.16 Peak Q position [A^-1] = 0.031081 Peak FWHM (Q) = 0.011906 Peak Integral Intensity = 0.29125 Prefactor = 0.29117 Position = 0.021975 Width 0.0041395
Summary results for population 4 This population was Diffraction Peak Contrast = 1 Peak profile shape = Gauss Peak D position [A] = 66.395 Peak Q position [A^-1] = 0.094634 Peak FWHM (Q) = 0.040201 Peak Integral Intensity = 0.011818 Prefactor = 0.36884 Position = 0.071014 Width = 0.015045
*************************************************
Fitting data with one input data set¶
Select “data controls” radio button. Select data (‘Test Data’) and push red button “Add data”
Name the data “Alumina powder” in the “User name” field.
Let’s also select the background immediately here. Set cursor (square) to area of flat background (around point 100) and read value of intensity there from the reader below the graph. It should be around 0.12 or so. Type 0.11 into the “Bckg” field and check the “Fit?” checkbox. Note that the Min and max fields appeared and are set to 0.1 and 10x the value of our estimate. Uncheck the “Fit?” checkbox so the background is NOT fitted, when we run this next time…
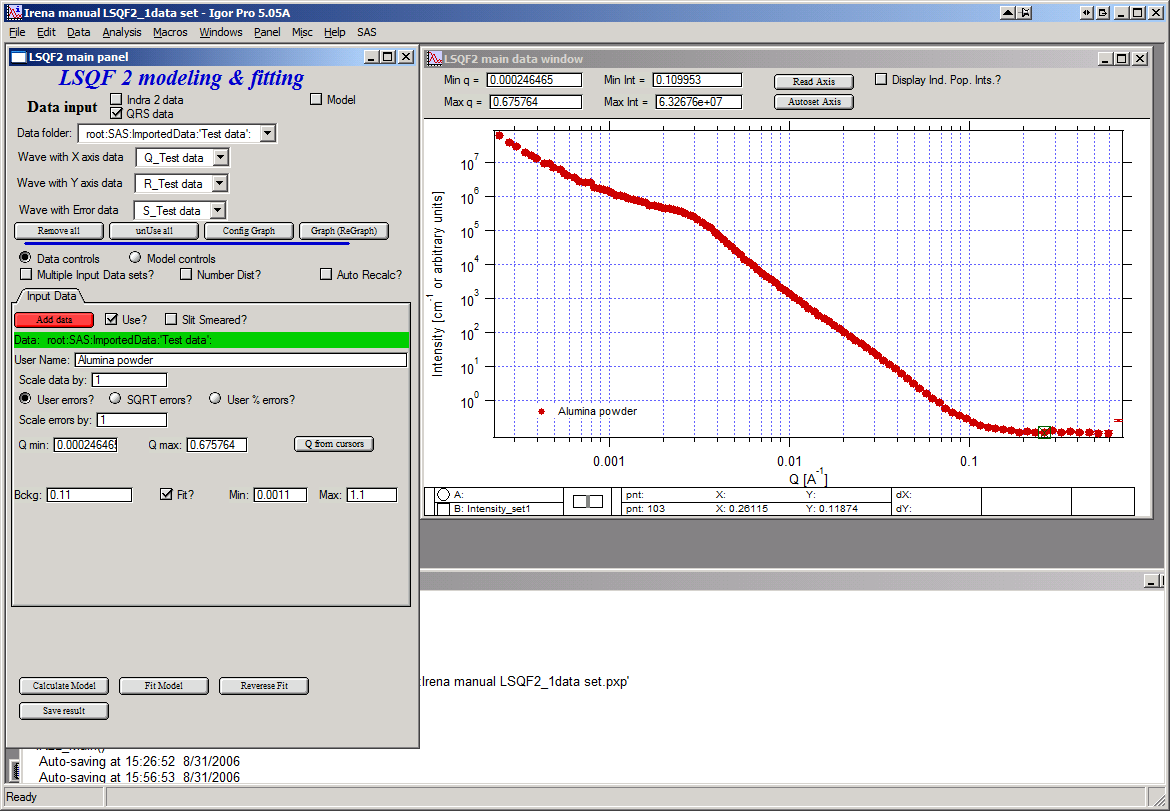
Now, let’s go to “Model controls”. Check the radio button “Model controls”. Check the checkbox “Auto recalc”. Make sure the “Interferences” checkbox is unchecked. Make sure that “Use?” checkbox for Pop 1 is checked and for all the others is unchecked.

The model (default values) is going to be calculated.
Let’s decide, that this population will be the larger stuff, dominating the data. This means the Guinier knee at around 0.003 A-1. Also, since these data are not calibrated (powder sample), we can leave contrast to default value of 100. But if data would be meaningfully calibrated, correct contrast needs to be used here… Let’s change values little bit to get better estimate of parameters… Reasonable starting point is may be with Min size ~ 100, Mean ~ 450, and Std. dev ~ 0.5 :
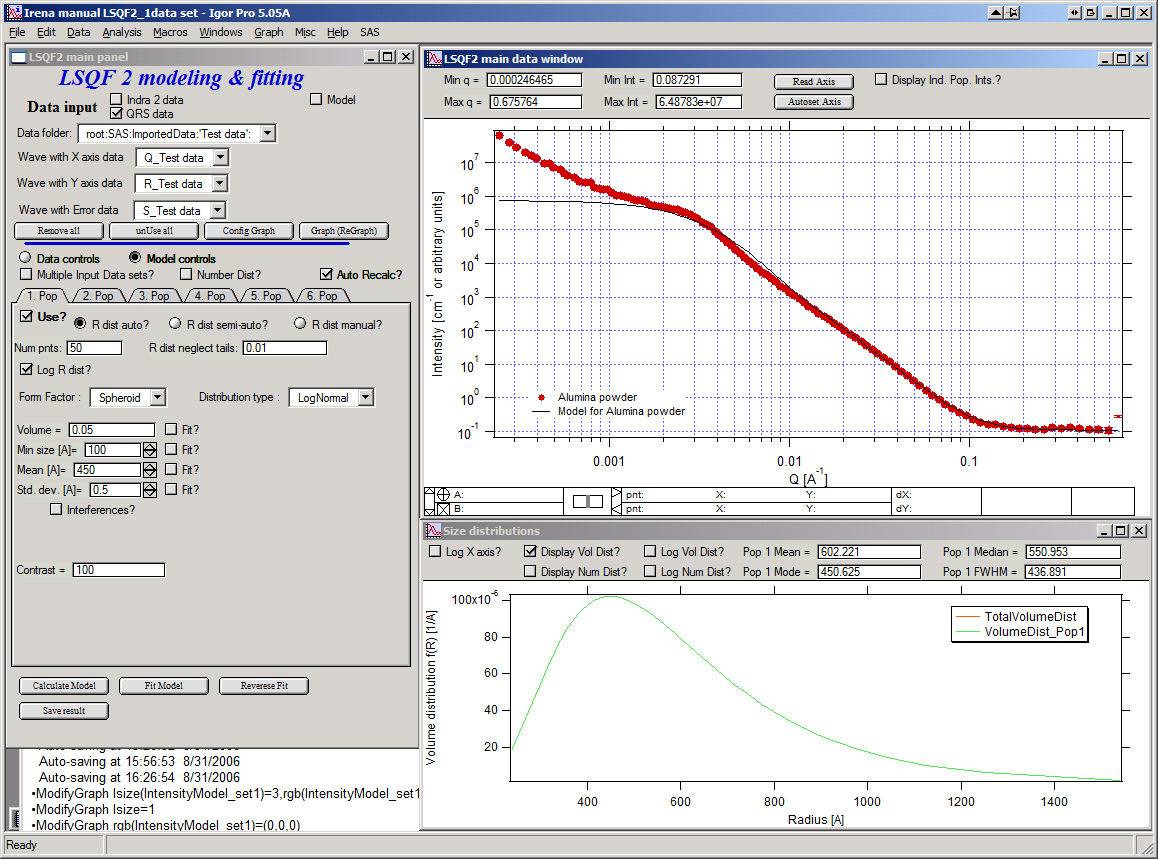
Now we need to select fitting range for this population… Check the “Data controls” Use cursors to select in the graph input data between point 30 and 73 and push button “Q from cursors”. This will set the Q min and Q max values.
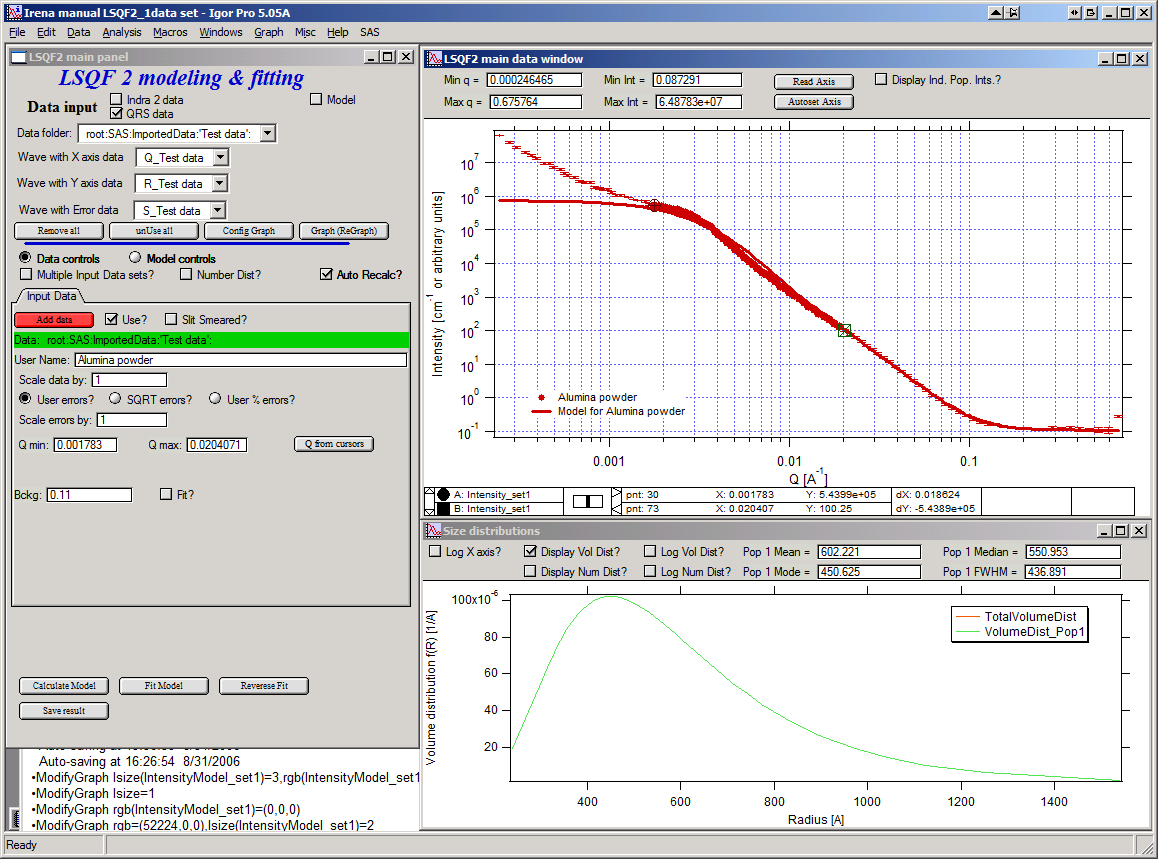
Make sure the background “Fit?” checkbox is unchecked here…
Now, let’s select parameters to fit. Background is not appropriate for this subset of data. Select “Model controls” again. Check “Fit?” for Volume, Min size, Mean and Std Dev. Values for fitting limits should be set to relatively wide range.
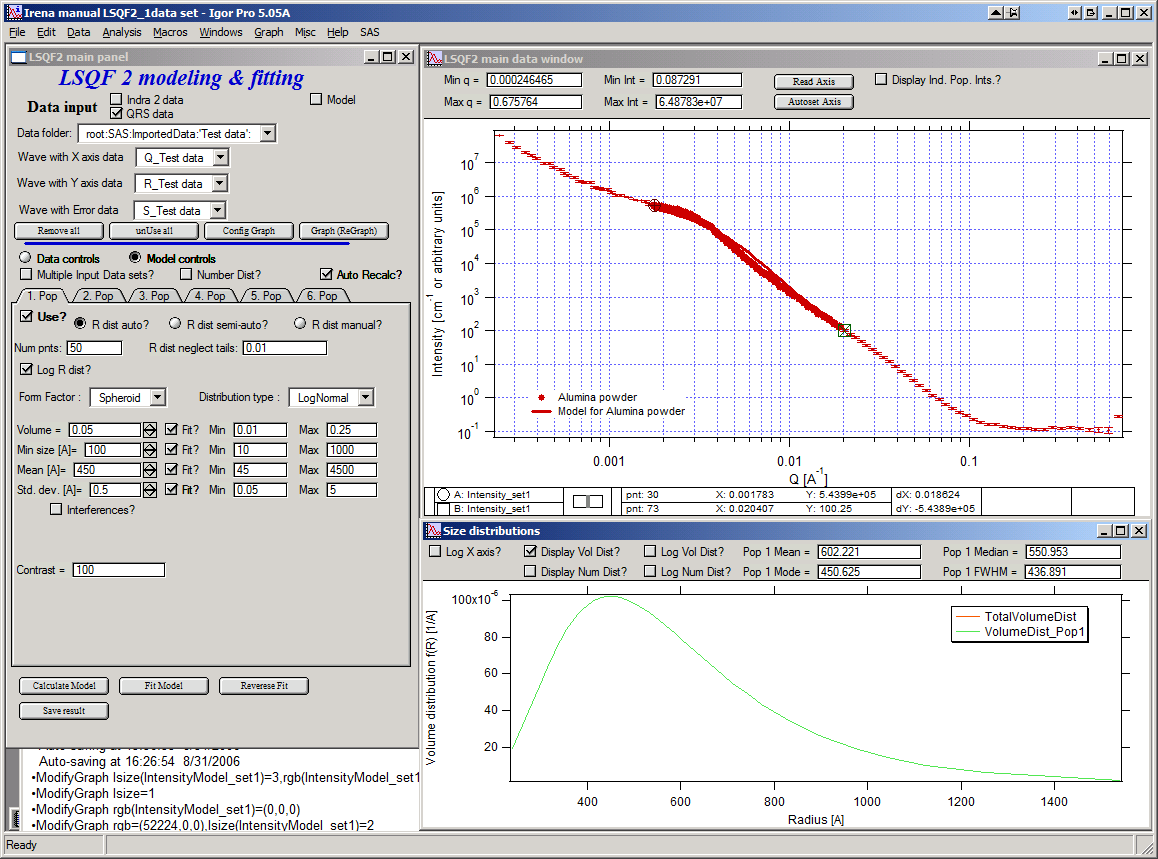
Now push button “Fit model” at the bottom of the panel. The model should fit after few iterations…
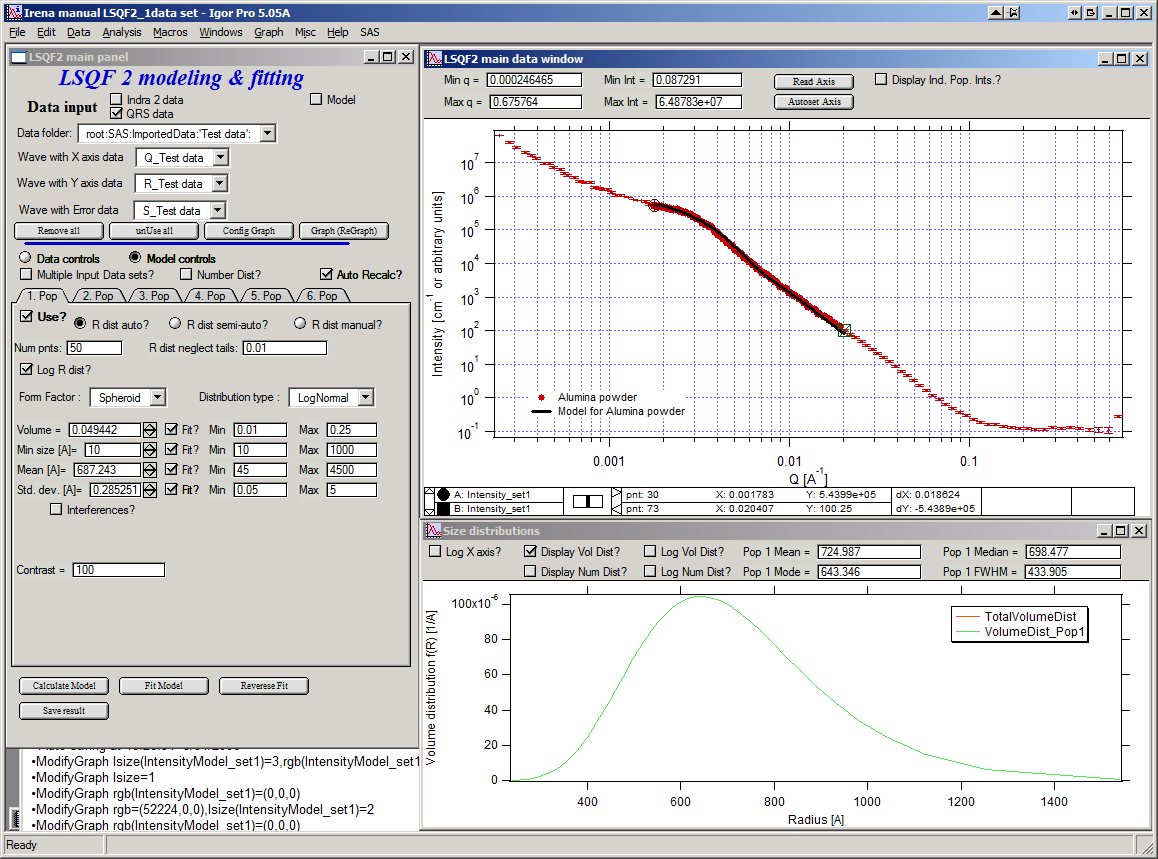
Now we will add other population (smaller particles). Uncheck all “Fit?” checkboxes on this Pop tab.
Select Pop 2. tab. Check “Use?” checkbox here. To see whole q-range, go back to “Data controls” and change Qmin and Q max to smaller/larger values (0.0015 and 0.5). Now come back to “Data controls” and let’s see, where the population 2 should be. Easiest achieved by unchecking “Use?” for population 1 and then the model in the graph is only for population 2. We want to use this population to describe data at around 0.05. So we need to move the mean to smaller sizes… This can be achieved by setting Mean to around 80 and reducing volume to about 0.01. Now check again “Use?” for population 1.
Check “Fit?” for Population 2 volume and Mean and fit the data by “FitModel” button.
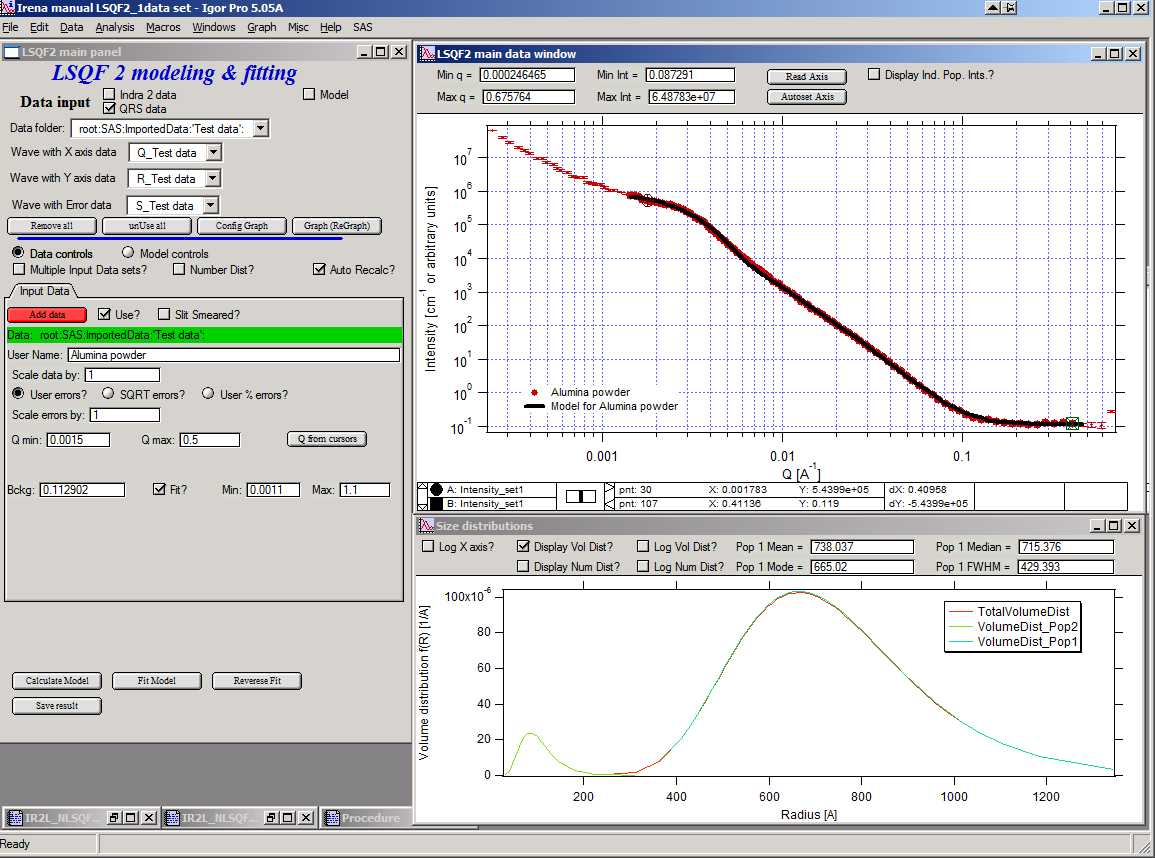
Now we need to do final fitting of all meaningful parameters at once… There are now 3 places, where we need to select what will be fitted – but potentially could be even more… So let me review where the fitting parameters can be:
Data Controls – fitting of background
Model controls - Population tabs – fitting of distribution parameters (and volume, potentially interference parameters) – here we have two of these to check.
Model controls – Form factor panels - Potentially we could have for each population form factor parameters fitted, these need to be selected by reselecting again on each Population tab the form factor, which brings up (if appropriate) the appropriate panel..
Good luck finding all of the parameters… You need it.
Anyway, select background, Volume for each f the populations, Mean size, and Std deviation. Try to fit to the data from 0.0015A-1 to 0.5 A-1… With little bit of luck (and a lot of calculations) you should get result similar to one below:
Uncertainty evaluation¶
This script enables to analyze uncertainties of parameters of the Modeling II, same method as Unified fit (chapter 6.6). There are two different types of analysis one can imagine:
Effect of input data uncertainties on the results. This analysis is done by running same fitting analysis (with all parameters fitted) on variations of data. These variations are created by adding Gaussian noise on input data. The Gaussian noise is scaled to have same standard deviation as input data uncertainties (“errors”). Analysis on these randomly modified data is run multiple times and statistical analysis on the results for each parameter is performed.
Stability of each parameter separately. This is bit more complicated - analyzed parameter is fixed, step wise, in range of values user specifies. Other user-selected parameters are fitted and chi-square values are recorded. After the analysis, this dependence is analyzed and based on statistical analysis (number of fitted points and free parameters) the uncertainty of the parameter is estimated. This method is based on chapter 11 “Testing the fit” in “Data Reduction and Error Analysis” P. Bevington and D. K. Robinson, available here (http://hosting.astro.cornell.edu/academics/courses/astro3310/Books/Bevington_opt.pdf). The calculation of Chi-Square target based on number of degrees of freedom is obtained by using data from table C4 in this book and approximating them with polynomial function for ease of calculation.
Here is example of results:
**********
Effect of data uncertainties on variability of parameters
root:SAS:ImportedData:S4_0055_sub:
Run 20 fittings using data modified by random Gauss noise within “Errors”. Note, that adding noise on data increases chi-square significnatly.
To get following statistical results
Chi-square values : average +/- st. dev. = 180 +/- 19
Volume_pop1 : average +/- st. dev. = 0.114 +/- 0.006
Volume_pop2 : average +/- st. dev. = 0.0862 +/- 0.0019
GMeanSize_pop1 : average +/- st. dev. = 6.9 +/- 0.5
GMeanSize_pop2 : average +/- st. dev. = 26.0 +/- 6.9
GWidth_pop2 : average +/- st. dev. = 51.8 +/- 3.9
StructureParam1_pop1 : average +/- st. dev. = 9.6 +/- 0.4
StructureParam2_pop1 : average +/- st. dev. = 0.212 +/- 0.018
Background_set1 : average +/- st. dev. = 0.00267 +/- 0.00064
************
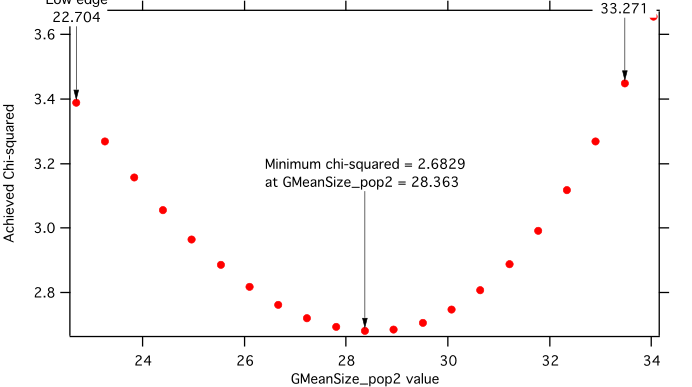
Moldeling II Evaluation of parameter GMeanSize_pop2
Method used to evaluate parameter stability: Sequential, fix param
Minimum chi-squared found = 2.6829 for GMeanSize_pop2 = 28.363
Range of GMeanSize_pop2 in which the chi-squared < 1.2623*2.6829 is from 22.704 to 33.271
**************************************************
“Simplistic presentation” for publications : >>>> GMeanSize_pop2 = 28.4 +/- 5.3
**************************************************
NOTE: you need to make sure the fitting limits are set widely enough as the fit may abruptly stop when these are violated. The Help in the panel provides many more details.
Fitting data with multiple input data set¶
Assumption of this chapter is, that you can already fit data with one data set. Only differences caused by adding other data sets are pointed out here. Not everything can work easily though - scripting does not work and analysis of the parameters uncertainties has not been tested yet.
Changes in Data controls
When “Data controls” AND “Multiple Input Data Sets?” are selected, up to 10 input data sets can be loaded at the same time in the tool. Each Data set has all of the controls as the first one, including separate background. Note, that if the background is to be fitted, checkbox needs to be selected on its tab.
If “Different contrasts for data sets” is selected, separate contrast needs to be input for every population and every population. This can be excessive number of contrasts. It is typically suitable for anomalous SAXS data evaluation.
Note, that the selection of number/volume distribution is used for all of the populations at the same type. You cannot mix number and volume distributions at the same time.
Note, that you can use one or more of the input data sets at the same time. If you unselect the “Use?” checkbox on any data tab, all parameters stay in the tab. Therefore you can mix-and-match data any time from any of the 10 populations.
Changes in Model controls
All controls stay the same. Contrast field will change reflecting selections: if “Different contrast for data sets” is not selected only one Contrast will appear, if it is selected, “Contrast data X” will appear, if Data X are set to be used. This appears on EVERY population tab. You need to go and check the contrasts for every population.
General comment
Please, remember, that with more data sets, this will be much slower. Setting up parameters for this complicated fitting space can be intimidating and very much complicated. You need to go through all of the used tabs in both Data controls and Model controls.