Analytical models - obsolete¶
Use :ref:`System Specific Models <System_specific_Models>` which is tool which replaced Analytical models
This tool provides GUI for different models: Debye-Bueche, Treubner-Strey, Ciccariello-Benedetti
Debye-Bueche model for modeling structural in homogeneities in the gels.
Treubner-Strey model for modeling of small-angle diffraction
Ciccariello-Benedetti for coated smooth surfaces
All models can be combined with low-Q Single Unified level. The controls have now four tabs – one for Unified level, one for Bebye-Bueche, one for Treubner-Strey, and one for Ciccariello-Benedetti. It is possible to combine them together, but it is not likely physically meaningful.
For explanation of the Unified level control, please see Unified fit. In version 2.54 I have added ability to link RgCo to parameters from Debye-Bueche and Treubner-Strey models. Also I have (pre request) added plot of residuals.
Debye-Bueche model for gels¶
The theory is implemented in following form:
where \(K = 8 \pi ^2 \lambda^{-4}\)
Parameters of the gel are then the corrL – correlation length and \(\varepsilon\). The model also allows low-q power law to be fitted and subtracted from data as well as flat SAS background. The low-q power law slope has 2 parameters (slope and prefactor) and background has one. All can be fitted.
NOTE: August 2012 user identified typo in the formula, which was used:
Based on provided citations, this formula needed corrL3 not corrL2 as was used in original implementation. As of now I am looking in the source of this error (which dates to about 2003). Currently there are not really clear, refereed publications I could base the decision on here. Actually, the one referred publication (my own) I have cites the “wrong” formulas. If you have any citation or opinion here, let me know.
The best I can is get at this time is following citation from Hammouda, NIST, web presentation:
Quoting: The Debye-Bueche model is used to describe scattering from phase-separated (two- phase) systems. Here also correlations are characterized by an e-folding length ξ. The pair correlation function is give by (Debye-Bueche, 1949):
The scattering cross section is obtained by taking the Fourier transform to obtain:
The prefactor can be expressed in terms of the volume fraction φ and contrast factor \(\Delta \rho^2\) as:
The Debye-Bueche model is obtained as a special case of the Teubner-Strey model for
very large d-spacing (d>>ξ).
******
This is the main screen:
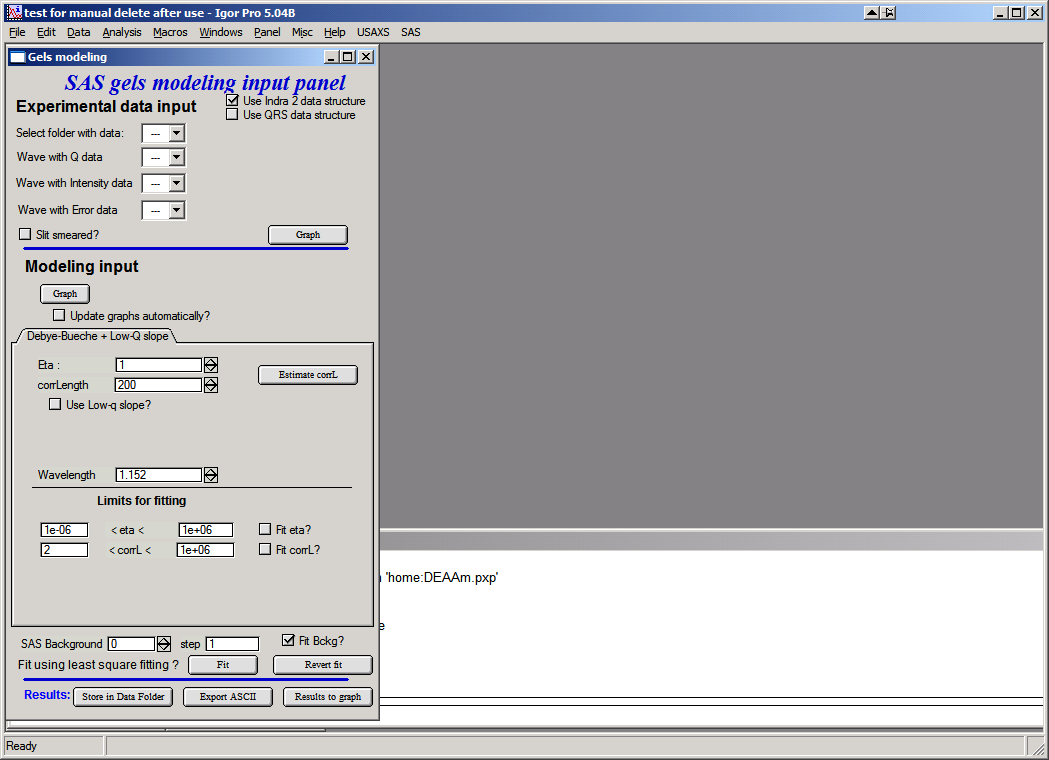
In the top part are standard data selection tools . Data can be selected, user can use either pin-hole type data (or desmeared USAXS data) or slit smeared data. Results are the same, the model is slit smeared with slit length if slit smeared data are used.
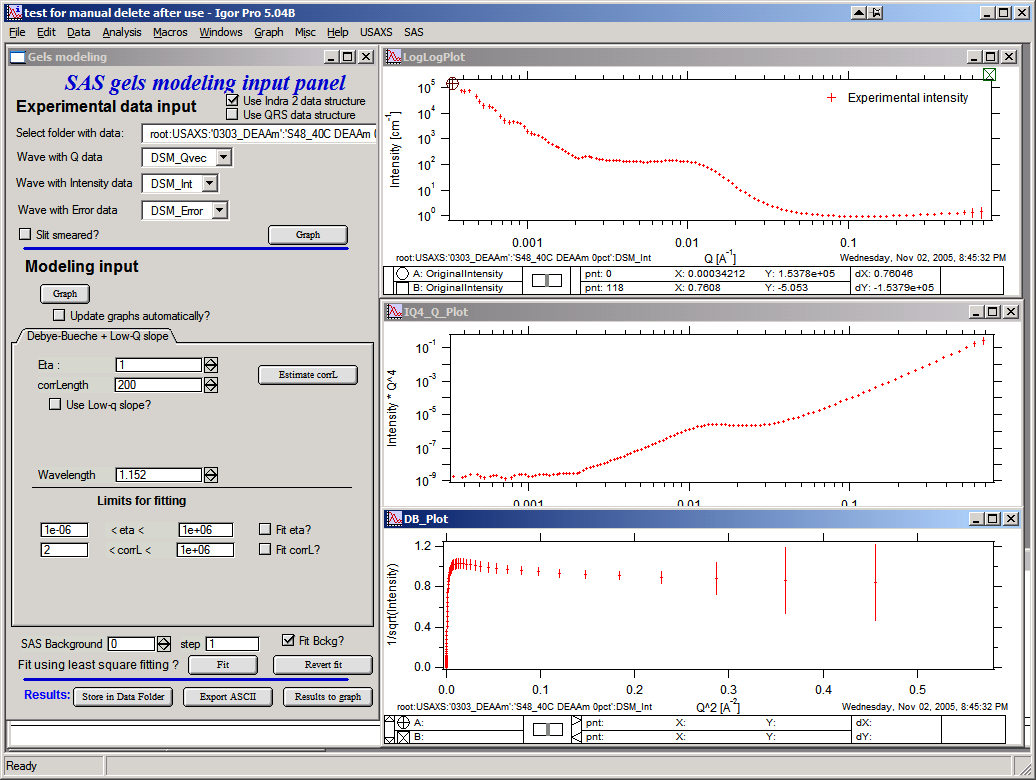
This is how the screen looks like with data selected. Note three graphs:
Top is log-log, middle is I * q4 vs q, and bottom is 1/sqrt(Intensity) vs q2. Data selection for fitting purposes is in the top graph…The other two are only for informational purposes.
Controls:
Top button “Graph” loads data into the tool and creates the graphs.
Lower Button “Graph” will calculate model and place result in the graphs.
“Update graphs automatically” will recalculate model after every change of any parameter in this tool. Useful on fast machines.
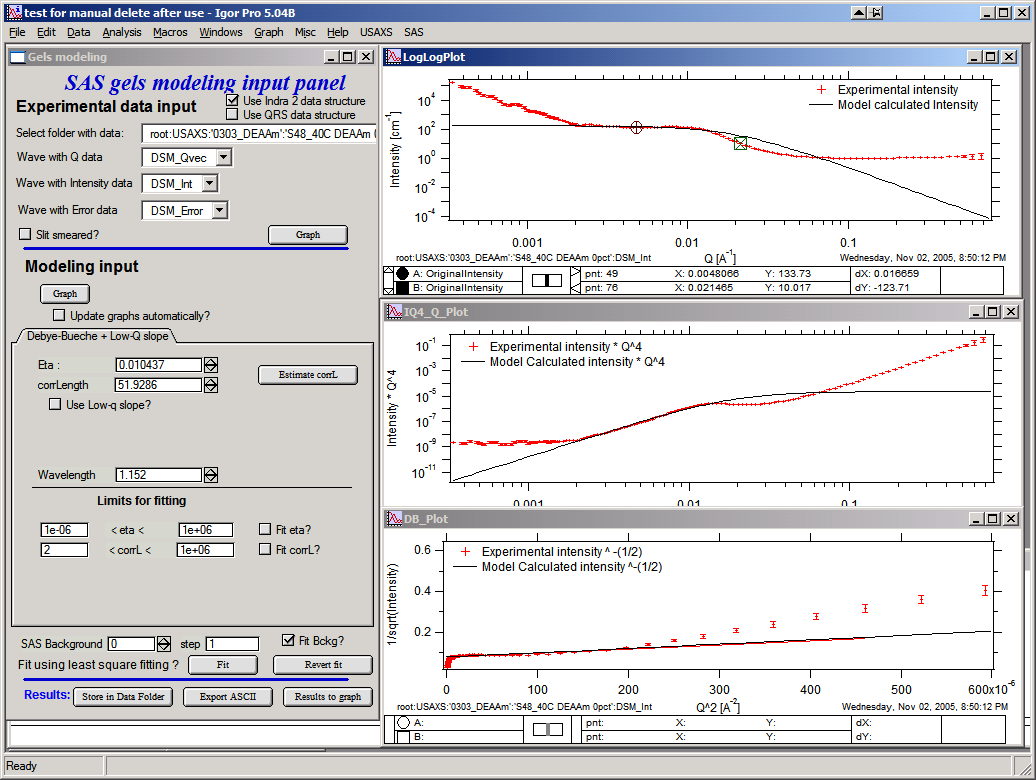
Eta and corrLength – model parameters. Can be estimated using the button “Estimate” if the knee area is selected first in the top graph:
Checkbox “Use low-q slope” will enable controls for low-q power law slope. One can again select range of data where the power law dominates and Estimate slope with the button.
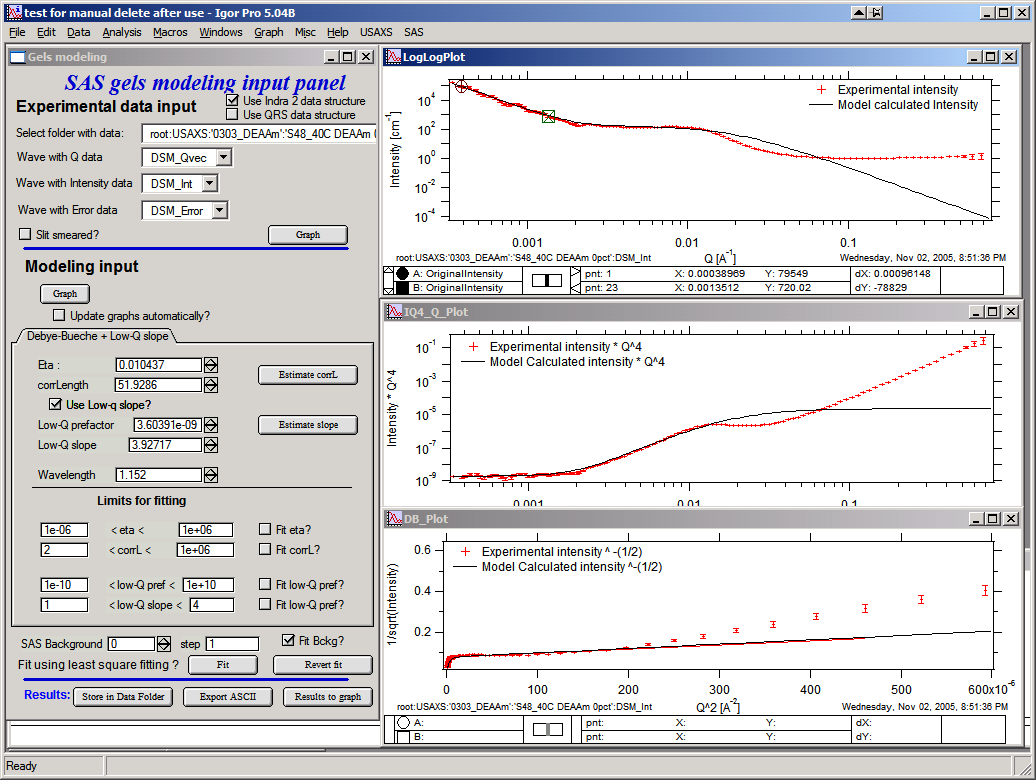
Limits for fitting should be set, if needed, to sensible numbers. The checkboxes with “Fit …” allow selection of parameters which are going to be fitted using standard Igor least-squares fit.
Last item is “Background”, which should be reasonably guessed and then fitted as one of the parameters:
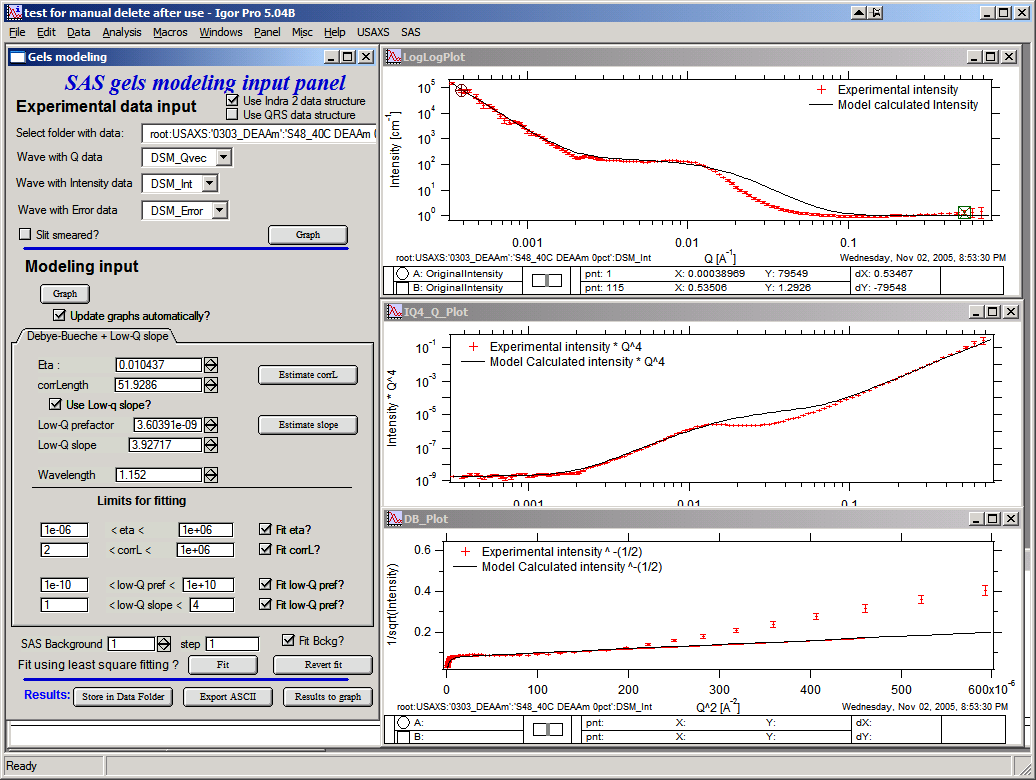
Now with good starting guesses one can fit the model – using the “Fit button”
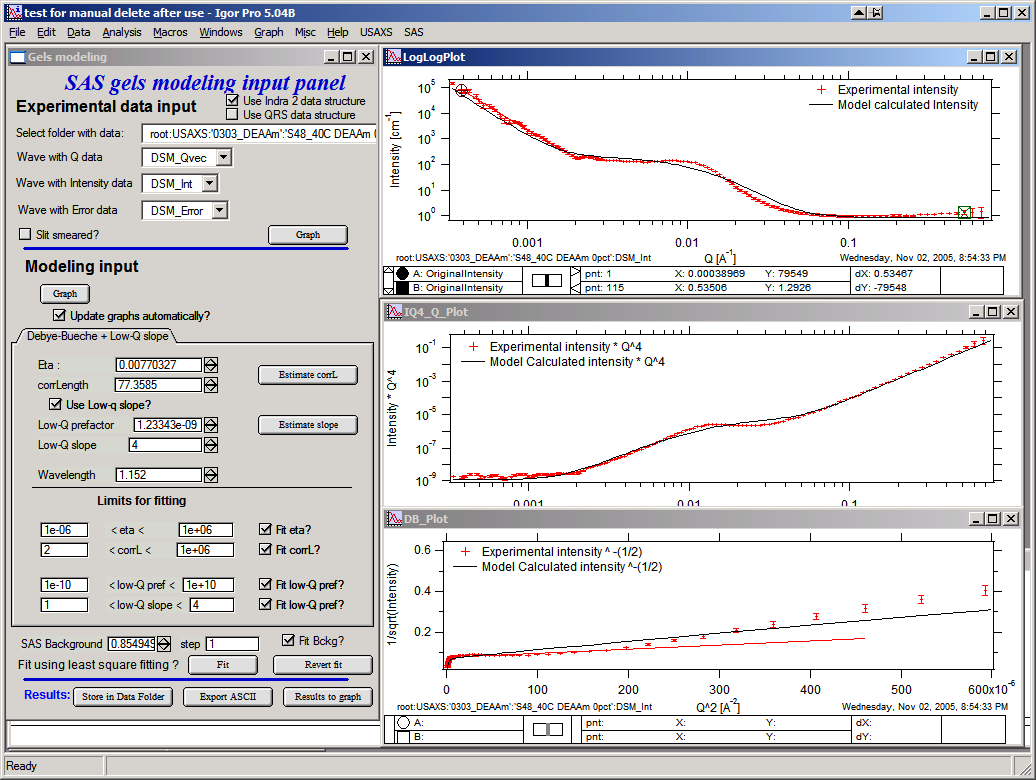
This is the best fit this model does to these data (note the misfit, this is not probably the best model…).
Buttons:
Revert fit – use to reset the last set of parameters after bad fit which “lost it’s way”…
Store in Data folder will save model data (waves with wave notes) for further use. It copies them into folder, where the data came from. Can be plotted, exported, reloaded in this tool, and mined for numbers later.
Export ASCII will export model as ASCII from Igor.
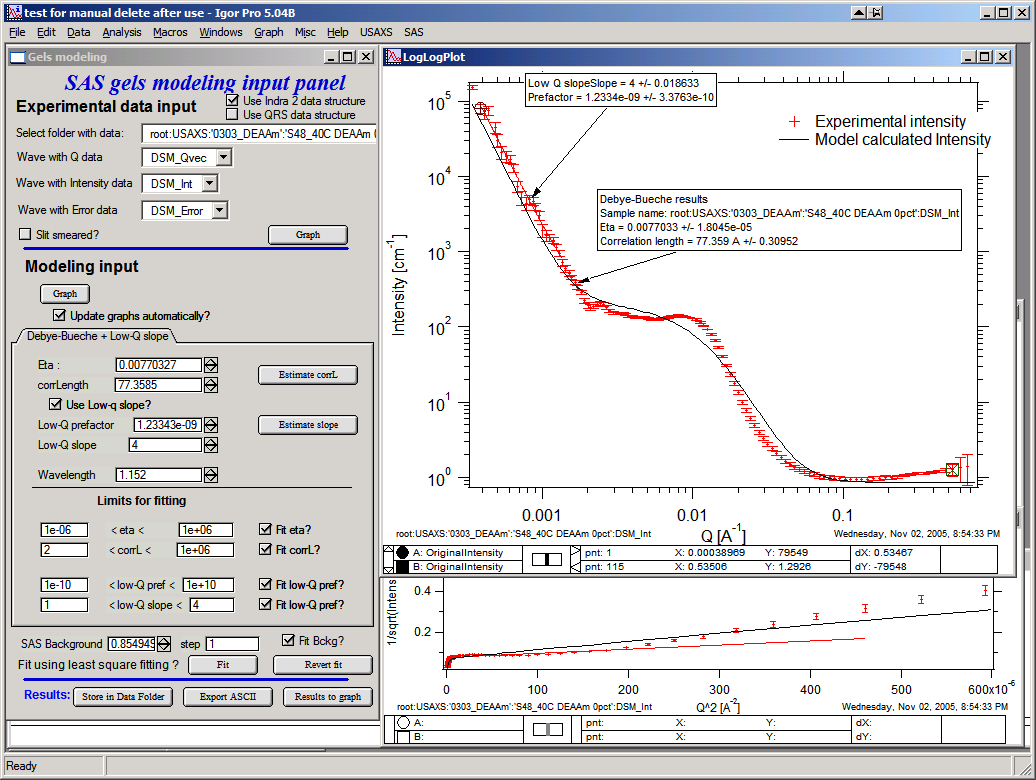
Results to Graph will paste results into graph for better view:
Treubner-Strey for small-angle diffraction¶
Treubner-Strey model follows the publications : Teubner, M; Strey, R. J. Chem. Phys., 1987, 87, 3195 and Schubert, K-V.; Strey, R.; Kline, S. R.; and E. W. Kaler J. Chem. Phys., 1994, 101, 5343.
The code is adopted form NIST SANS package. The formulas are:
Where A, C1 and C2 are parameters from the theory and TS is scaling factor.
Correlation length °ξ and repeat distance (d) are:
Example of the GUI with results:
Note, that only the parameters TS, A, C1, and C2 are user controlled. Parameter TS is added scaling factor, as there does not seem to be other way to scale the model to data.
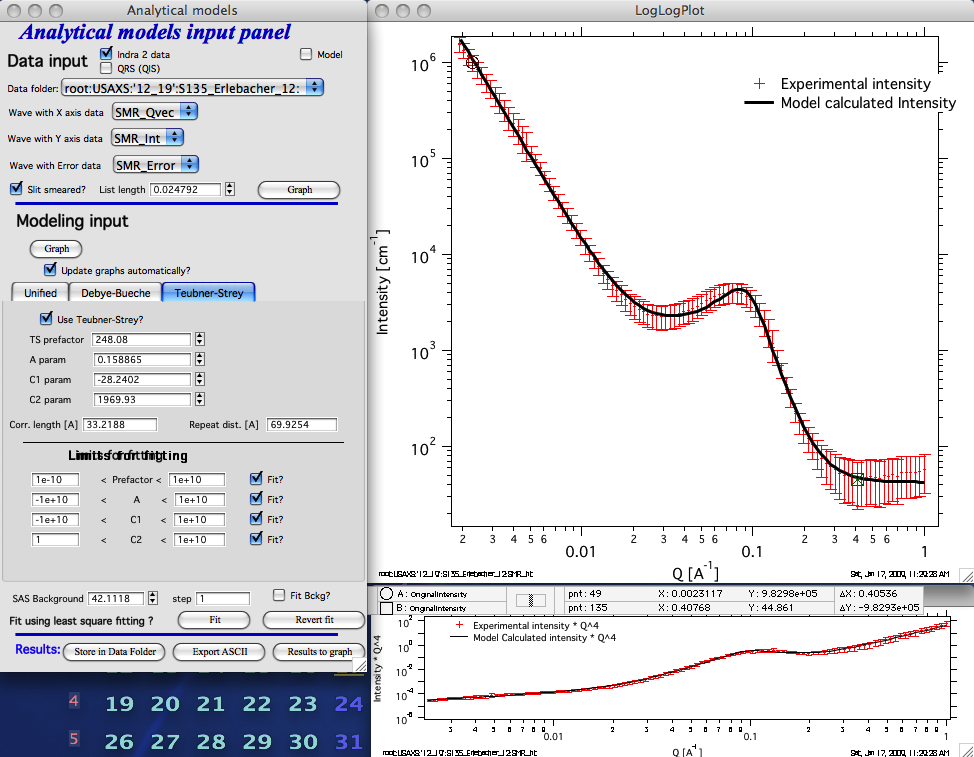
This is fitting to slit-smeared data for which Treubner-Strey model is the appropriate model to use.
Ciccariello–Benedetti model for coated smooth surfaces¶
This tools was coded using following manuscripts:
Benedetti, A., S. Ciccariello, Coated Silicas and Small-angle X-ray intensity behavior, J. Appl. Cryst (1994) 27, 249-256.
Pikus, S., E. Kobylas, and S. Ciccariello, Small-angle scattering characterization of n-aliphatic alcohol films adsorbed on hydroxylated porous silicas, J. APpl. Cryst. (2003) 36, 744-748.
And tested on experimental data provided by S. Ciccariello. Note, that the experimental data were only slit smeared and that I have found some interesting discrepancies between using finite slit length (an dusing internal smearing routines of Irena for slit smearing the model) and running provided specific code for slit smeared data (assuming infinite slit length). Simply put, the results vary depending on slit length and one needs to be careful on this. Please, read further…
In summary, this model assumes that on surfaces of porous media is present constant thickness and constant scattering length density layer. The surface of the film is assume to be always parallel with the surface of the solid. Basically, it is coated porous surface with very specific layer – since this is modification of Porod’s law, it is clear that the interfaces must be sharp. In this case the Porod’s Q-4 power law is modified by oscillatory behavior from which one can extract the thickness and scattering contrast of the film. For more details, please read the manuscripts.
Ciccariello-benedetti GUI:
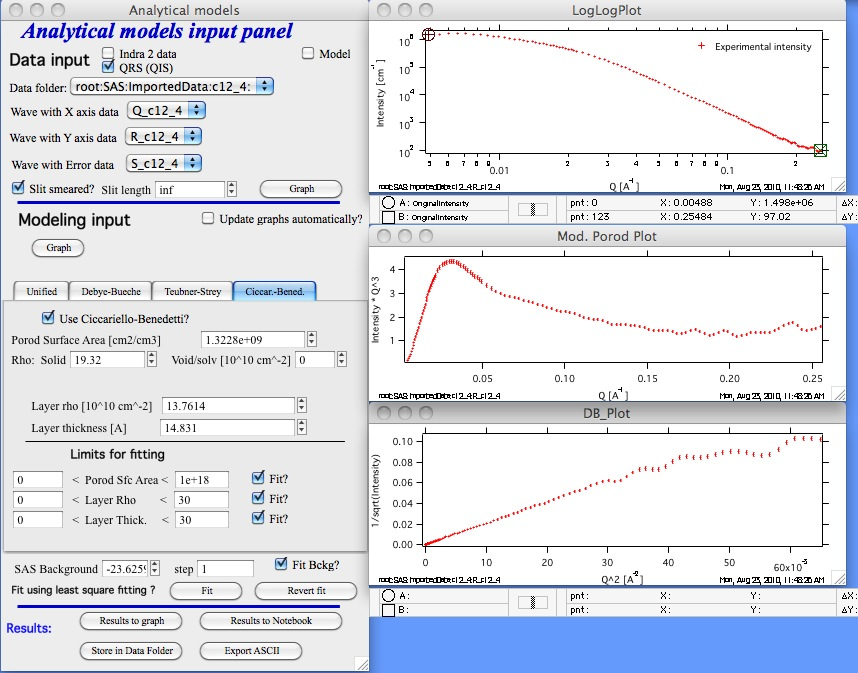
This is the control panel and loaded data for this method…
AT the top of the main panel is regular “Load data” selection. In this specific case ONLY (no other Irena tool supports infinite slit length) you have a choice of finite slit length and “inf” as infinite slit length. Also you can run this on data in pinhole configuration.
If you want to use this tool, select “Use Ciccariello-Benedetti” checkbox. Controls will appear.
The model has three main parameters, which can be fitted:
Porod specific surface area (area of the solid/void (solvant) interface. This is area of the interface without the layer on.
Layer rho (scattering length density)
Layer thickness
And the model has two parameters which area assumed to be known:
Scattering length density of the solid (rho) and scattering length density of the void/solvent (material which is inside the voids). If this is air, it is likely 0.
Note, that one needs to select also SAS background and set fitting limites and “Fit?” checkboxes as in other tools.
When user pushed “Graph” button next to data selection, three graphs get created.
Intensity vs Q graph. PLEASE NOTE, this is still the ONLY graph you can use to select the range fo data to be fitted.
Intensity * Q4 (or for slit smeared data as in the image above: Intensity * Q3). This is probably the best graph for this tool. Unluckily, making this one the “input” graph would make it cumbersome and complicated to use with other tools.
1/sqrt(Intensity) vs Q2
Rest of the controls works the same as usually.
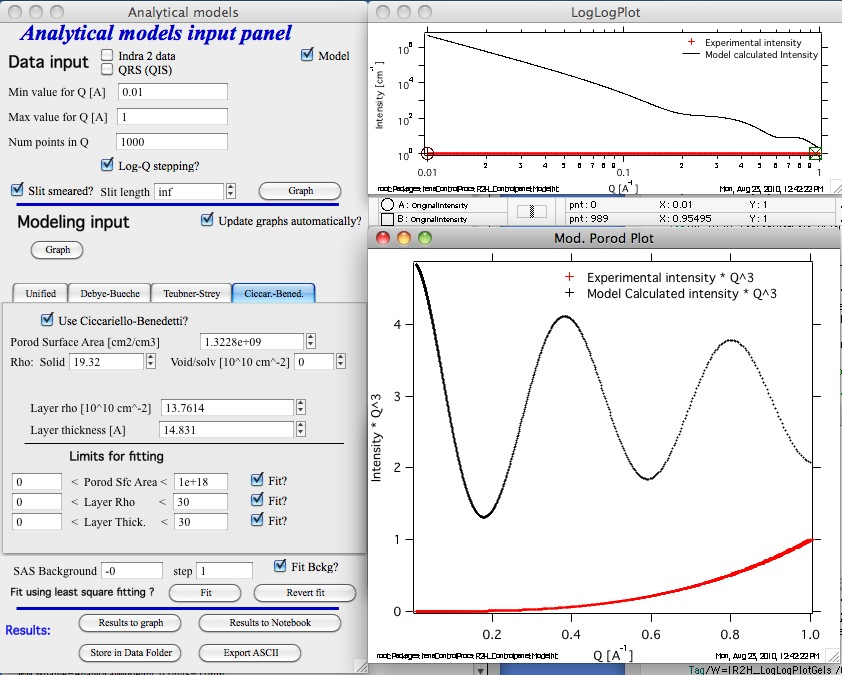
Finally, one may want to know how would “ideal” case of the system described by Ciccariello-Benedetti model looks like. You can do it easily by using the Modeling capabilities of this tool:
Here is slit smeared data set using the parameters from above, just with “Modeling” data only (no input data)
and here is the same set of parameters, just with pihole-colimated data input:
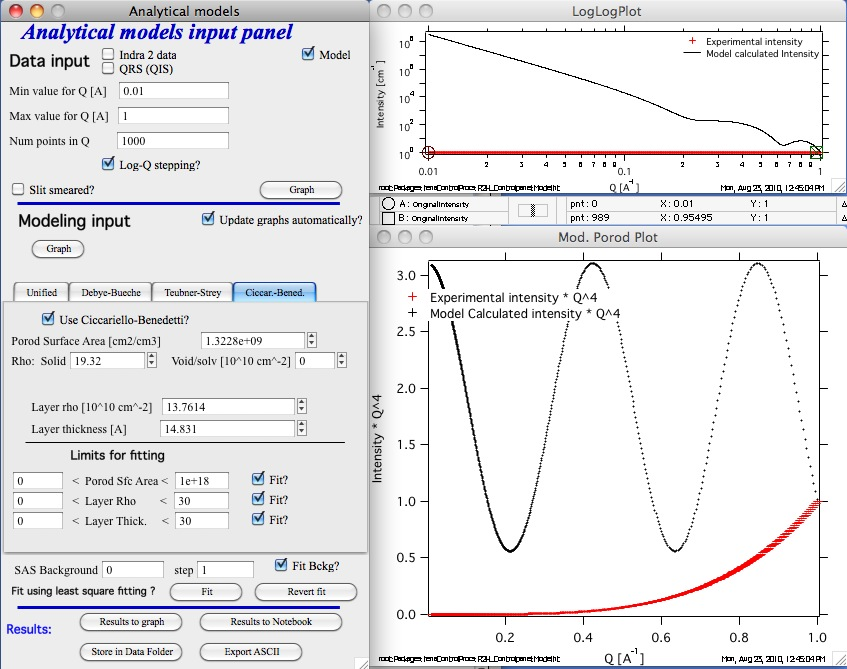
Note, that for these pinhole data the lower graph is set to be Intensity * Q-4.