Fractal model¶
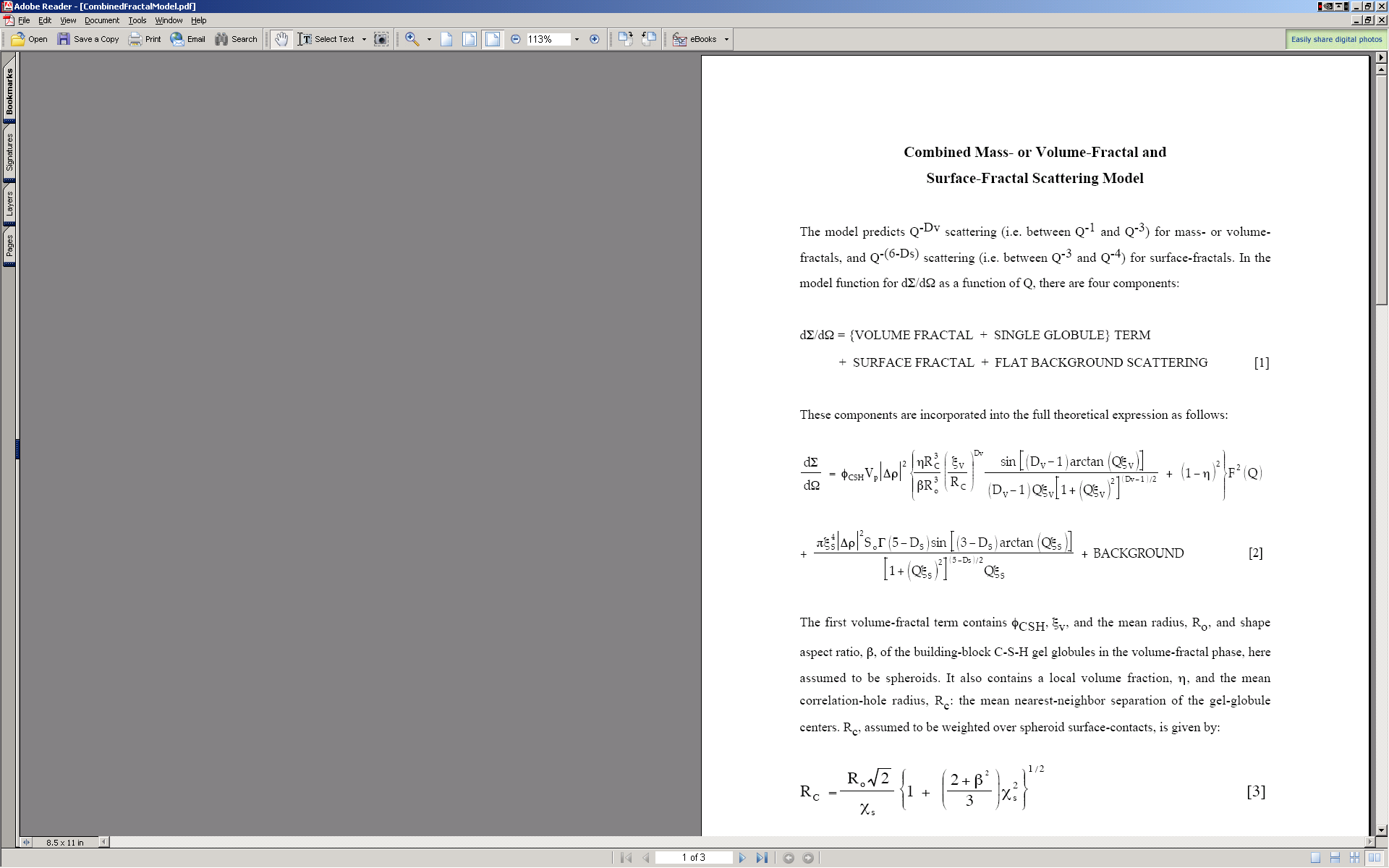
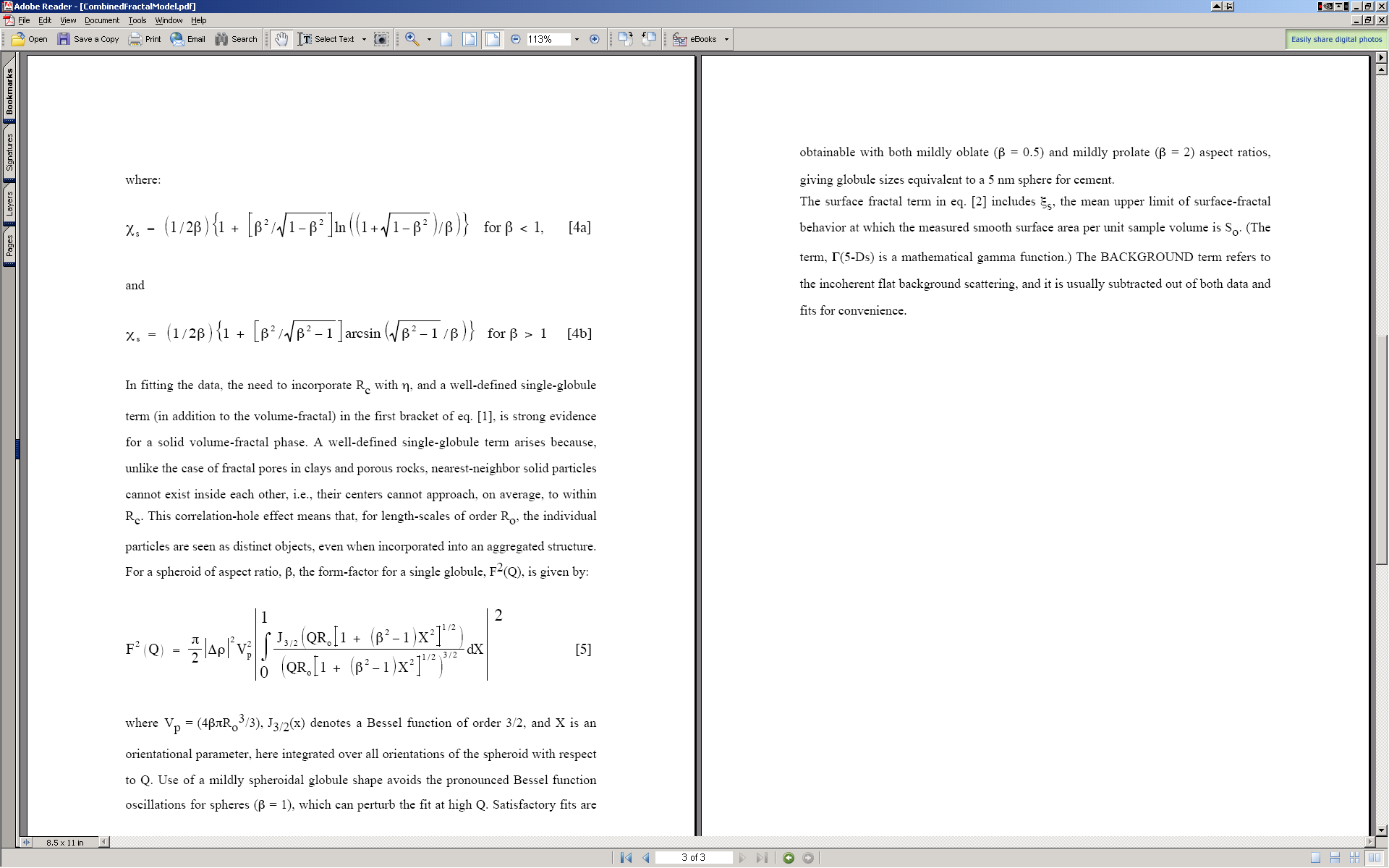
This model has been developed by Andrew J. Allen from NIST (Andrew.allen@nist.gov). The model allows to combine two volume and two mass fractals in much similar way as the Unified model does. The parameters from this model have advantage of being more “fractal-related” than the values from Unified. There is short pdf file included in the distribution, which served as basis for my design of this tool. Note, that this tool is actually port of Andrew’s original Fortran code into Igor, my code was verified to give same results as this Fortran code. Citation for this model all users should cite is: G. Gadikota, F. Zhang, A.J. Allen; “Towards understanding the microstructural and structural changes in natural hierarchical materials for energy recovery: In-operando multi-scale X-ray scattering characterization of Na- and Ca-montmorillonite on heating to 1150 °C,” (with supplementary material) Fuel, 196, 195-209 (2017). DOI: 10.1016/j.fuel.2017.01.092
- Important points to proper analysis using this model are:
Make realistic initial estimates of the parameters - including fixing any flat background term so it is effectively subtracted out from the model (can be refined slightly in a final fit). Porod law fitting can be used in an appropriate q-range to do this. This also has the advantage of providing a total surface area, St from which the “rough” surface-fractal surface area, Ssf, can be subtracted out to give the volume-fractal surface area, Svf, etc.
The eta parameter should also probably be fixed at ≈ 0.5 initially (again some final refinement can be considered when everything else is done.
The key problem for the user in all this is the following: If you have just one volume-fractal and one surface-fractal component, plus a background, there are in principle 9 fitting parameters. However, for each region of the scattering curve that has essentially one curvature, you typically only need 3 fit parameters for fit convergence in that region. So, to fit everything you really need to see at least 3 distinct regions of the USAXS/SAXS curve, and just 3 of the above parameters (a different 3 in each case) need to be dominant in each regime! A sensible trial of reasonable parameter values should be experimented with first, then fit parameters introduced progressively using what is known (at least qualitatively) to help discover and refine what is unknown quantitatively. Usually, I like to get semi-respectable fits for the whole curve, then focus on particular regions of the data to refine one set of component parameters, then fix most of these and move on to the next region, etc.
Note, that the short write up below was written for studies of cement and therefore some of the terms are material-specifically called.
Model description
Use
Important : If you are using USAXS data, these must be desmeared, not slit smeared. The tool will not “see” the slit smeared data. Turns out, it was really difficult to use slit smeared data for users.
I do not have included real fractal data, but for purpose of GUI description and function description, the included data should be sufficient.
Start the tool from SAS menu under “Fractal model”. GUI panel similar to all other tools appears, select “Use QRS data structure” and pick the data set available. The push “Graph” button to create graphs.
Note, that the “Subtract background” variable next to data selection allows to subtract known FIXED large background. The “SAS Background” at the bottom is similar term, but this one can be fitted during the fitting routine.
Select “Use mass fractal 1” for starters and other checkboxes as in image below:
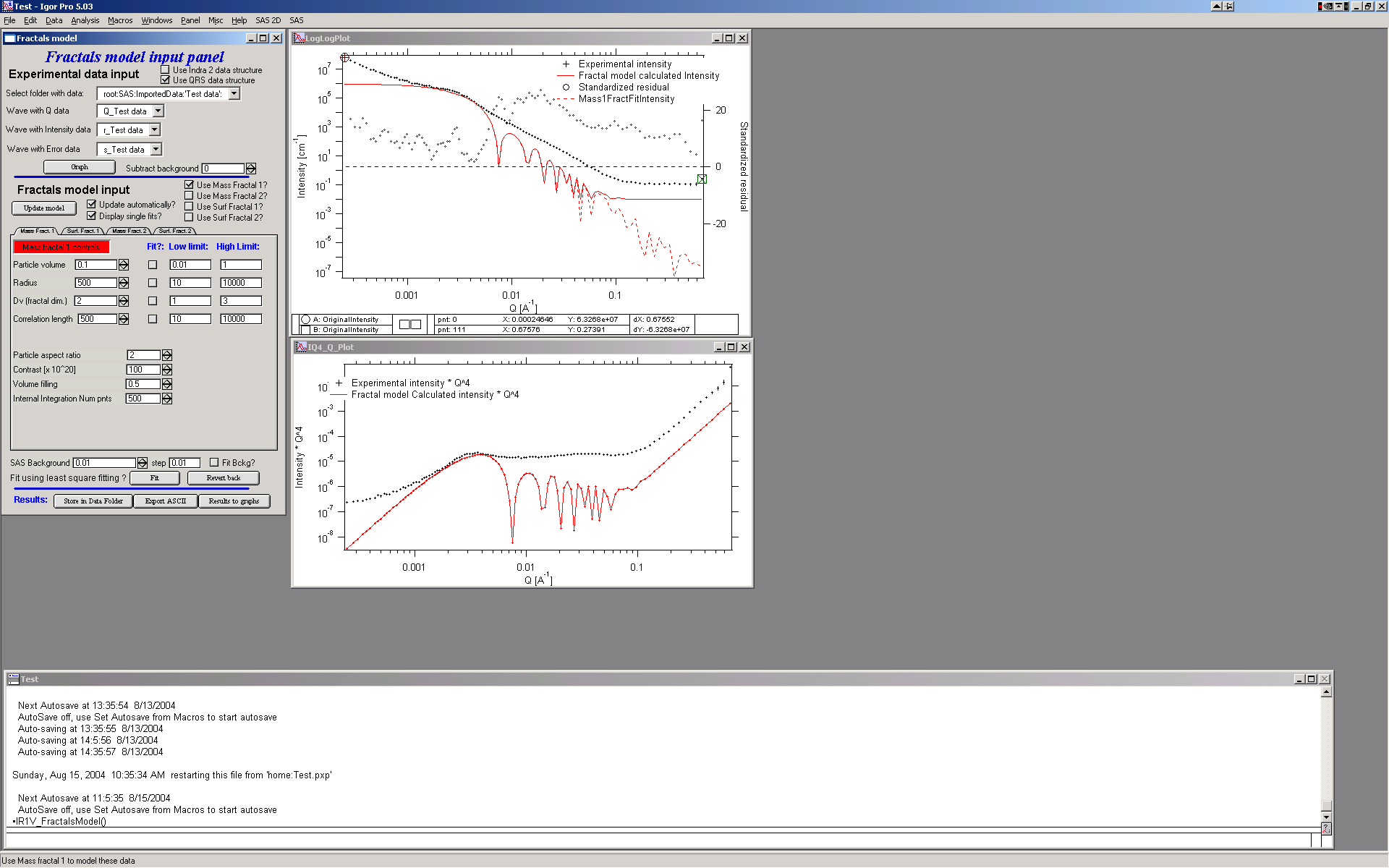
Note, that you can combine ANY combination of the two mass fractals and two surface fractals.
Comments on Mass fractal parameters:
Most parameters should be closely related to the ones mentioned above in description of the method.
Particle volume – volume of particles
Particle radius – size of the particle
Dv - fractal dimension
Correlation length – distance between the particles
Particle aspect ratio (beta) – Particles are spheroids with this aspect ratio - their dimensions are R x R x beta*R. Most often aspect ratio should be 1 if particles are approximately spheres (most common), larger than 1 are elongated spheroids (~cigars), lower than 1 for prolated particles (~disks). Note, that the code uses monodispersed Form factors (sphere or spheroid) and this results in Bessel function oscillations at high-q values. This is rarely realistic and unless there is Surface fractal at higher q values, model looks weird.
Use UF Particle Form Factor Starting from Irena version 2.70 you can choose checkbox “Use UF Particle Form Factor”. In this case code will use Unified Fit Sphere form factor which is approximate Form factor for sphere using Unified Fit model. Aspect ratio beta is not used (it is 1 since this is sphere). Note, in the figure below that there are no oscillations at high-q.
Polydispersity index When you choose checkbox “Use UF Particle Form Factor”, Polydispersity index (PDI) becomes available. This is value representing size distribution of primary particles. PDI=1 is completely monodispersed system, PDI=3 is when Porod’s region completely merges with Guinier area and highly polydispersed system has PDI up to 10. I expect typical systems to need PDI between 1 - 5
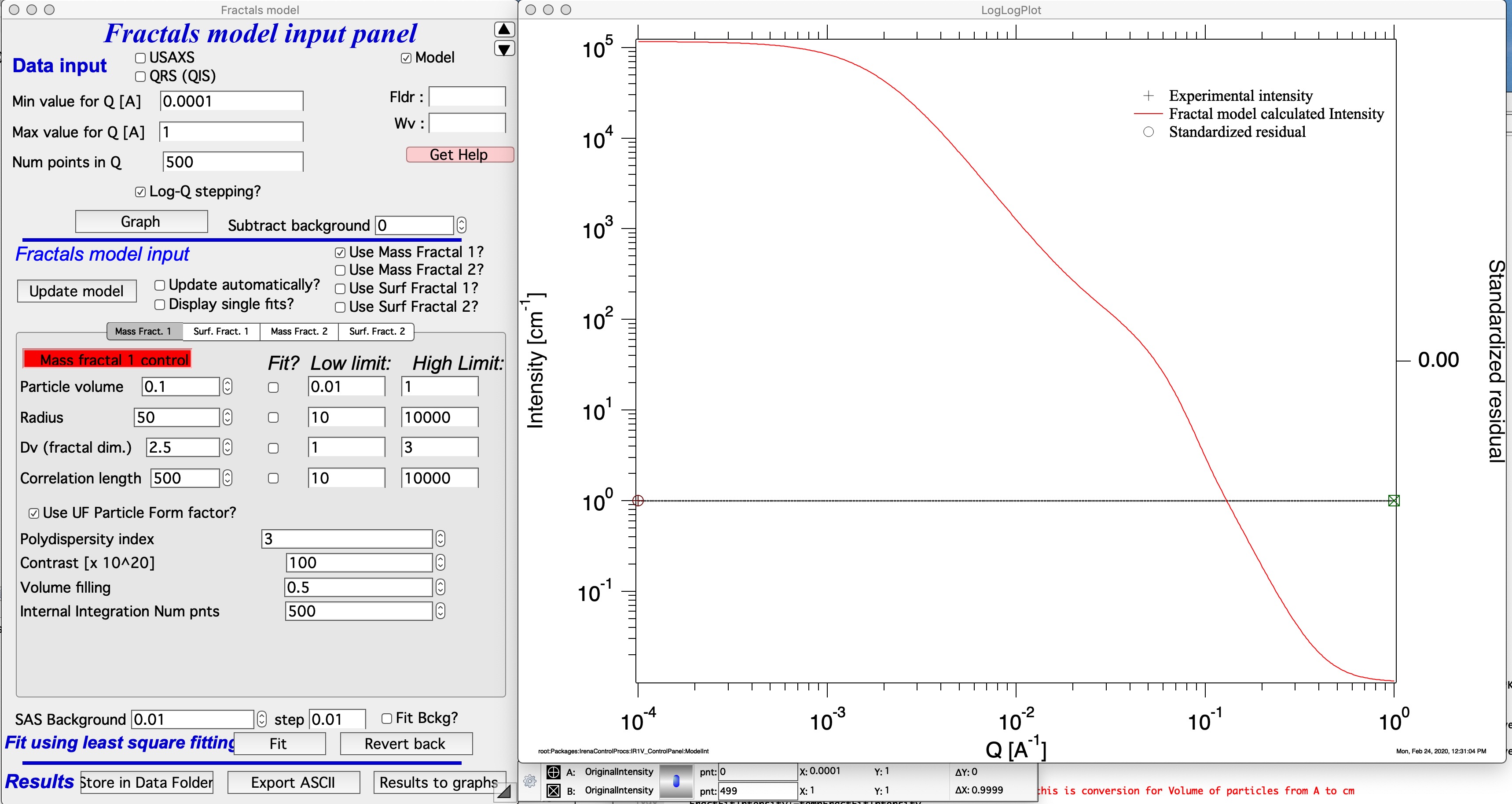
Contrast – contrast…
Volume filling – see above
Internal integration Num pnts – internal parameter. Number of point in the numerical integral which I use to calculate orientational average of the particle form factor. Small number of points (especially at high aspect ratios) can cause artifacts. Large number of points increases significantly calculation time. My suggestion is to lower the number of points to find a good starting conditions and for final fitting may be increase, or to recalculate for testing results with higher (double) number of points at the end – if no change is observed, the number of points is selected correctly.
Suggestions: check solution for particle aspect ratio 2 and 0.5, keep integral integration num of point reasonably high (over 100 for sure, likely around 500) and change it only if you seem to see artifacts. Keep volume filling between about 0.4 and 0.6.
Now select “Use Surf Fractal 1” and deselect the mass fractal:

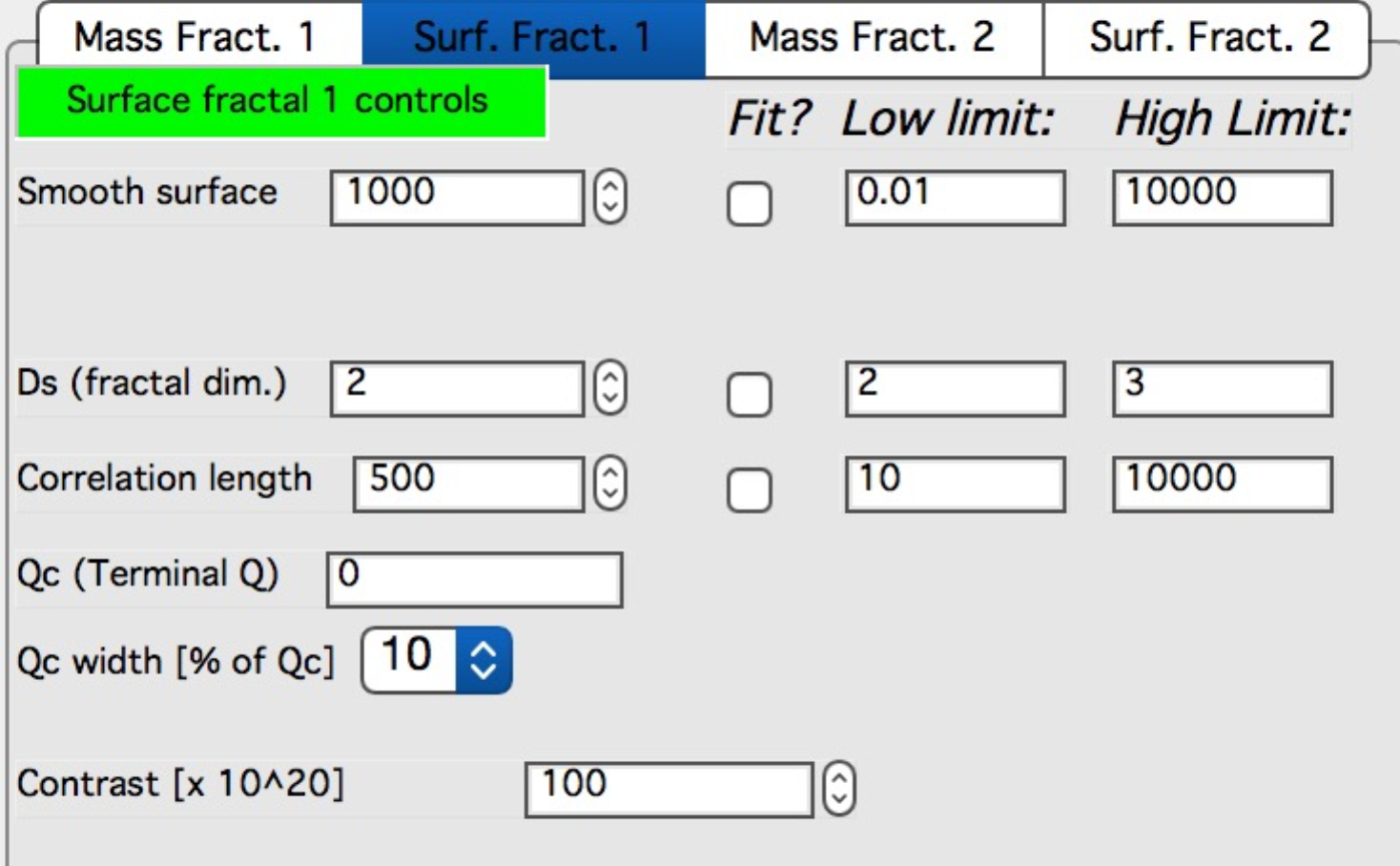
Bottom picture shows updated Surface Fractal panel.
Comments on surface fractal parameters:
Again, for meaning check the description above.
Smooth surface – limits of smooth surface as described above
Ds – fractal dimension
Correlation length – correlation length as described in the theory
Qc (Terminal Q) – Q value at which scattering reaches smooth surface and turns into Porod’s scattering (Int ~ Q-4).
Qc width [% of Qc] – smoothing parameter for the turn over in the function used to enforce the Qc. Typically 10%, can be 5, 10, 15, 20, and 25%.
Contrast - contrast…
Method of finding the solution is same as with Unified fit – first manually find good starting conditions and then select appropriate range of data with cursors and use fitting (select appropriate parameters to fit) to optimize data using least square fitting…