Form Factors & Structure factors¶
This is list of available form factor and structure factors in Irena package.
Form factors & their parameters¶
Form Factor |
Parameter |
ParticlePar |
|---|---|---|
Spheroid |
AspectRatio |
ParticlePar1 |
Intg_Spheroid |
AspectRatio |
ParticlePar1 |
Cylinder |
Length |
ParticlePar1 |
Disk |
Radius |
ParticlePar1 |
CylinderAR |
AspectRatio |
ParticlePar1 |
CoreShell |
CoreShellThick |
ParticlePar1 //skin thickness in Angstroms |
CoreRho |
ParticlePar2 //rho [10^10 cm-2] (not delta rho squared!!!) of core material |
|
ShellRho |
ParticlePar3 //rho [10^10 cm-2] (not delta rho squared!!!) of shell material |
|
SolventRho |
ParticlePar3 ParticlePar4 //rho [10^10 cm-2] (not delta rho squared!!!) of surrounding medium (air=0) |
|
CoreShellShell |
CoreShellThick1 |
ParticlePar1 //skin 1 thickness in Angstroms |
CoreShellThick2 |
PParticlePar2 //skin 2 thickness in Angstroms |
|
SolventRho |
ParticlePar3 //rho [10^10 cm-2] (not delta rho squared!!!) of surrounding medium (air=0) |
|
CoreRho |
ParticlePar3 ParticlePar4 //rho [10^10 cm-2] (not delta rho squared!!!) of core material |
|
Shell 1 Rho |
ParticlePar5 //rho [10^10 cm-2] (not delta rho squared!!!) of shell 1 material |
|
Shell 2 Rho |
ParticlePar6 //rho [10^10 cm-2] (not delta rho squared!!!) of shell 2 material |
|
CoreShellCylinder |
Length |
ParticlePar1 //length in A |
WallThickness |
ParticlePar2 //in A |
|
CoreRho |
ParticlePar3 //rho [10^10 cm-2] (not delta rho squared!!!) of core material |
|
ShellRho |
ParticlePar4 //rho [10^10 cm-2] (not delta rho squared!!!) of shell material |
|
SolventRho |
ParticlePar5 //rho [10^10 cm-2] (not delta rho squared!!!) of surrounding medium (air=0) |
|
CoreShellPrec |
CoreShellThick |
Is calculated for each size, so the average contrast of the core+shell is same as contrast of the solvent. |
CoreRho |
ParticlePar2 //rho [10^10 cm-2] (not delta rho squared!!!) of core material |
|
ShellRho |
ParticlePar3 //rho [10^10 cm-2] (not delta rho squared!!!) of shell material |
|
SolventRho |
ParticlePar4 //rho [10^10 cm-2] (not delta rho squared!!!) of surrounding medium (air=0) |
|
Fractal agg |
FrRadOfPriPart |
ParticlePar1 //radius of primary particle |
FractalDim |
ParticlePar2 //Fractal dimension |
|
SphWHSLocMonoSq |
Distance for HS model as ratio to part radius |
ParticlePar1 //ratio |
Fraction |
ParticlePar2 //Hard Spheres volume fraction |
|
Janus CS Mic 1 |
particle size |
Is total size of the particle (R0 in the figure in description) |
Shell_Thickness |
ParticlePar1 //shell thickness |
|
SolventRho |
ParticlePar2 //rho for solvent |
|
CoreRho |
ParticlePar3 //rho for core material |
|
Shell1Rho |
ParticlePar4 //rho for shell 1 |
|
Shell2Rho |
ParticlePar5 //rho for shell 2 |
|
Janus CS Mic 2 |
particle size |
Is shell thickness!!! |
Core_Size |
ParticlePar1 //Core Size |
|
SolventRho |
ParticlePar2 //rho for solvent |
|
CoreRho |
ParticlePar3 //rho for core material |
|
Shell1Rho |
ParticlePar4 //rho for shell 1 |
|
Shell2Rho |
ParticlePar5 //rho for shell 2 |
|
Janus CS Mic 3 |
particle size |
Is core radius) |
Shell_Thickness |
ParticlePar1 //shell thickness |
|
SolventRho |
ParticlePar2 //rho for solvent |
|
CoreRho |
ParticlePar3 //rho for core material |
|
Shell1Rho |
ParticlePar4 //rho for shell 1 |
|
Shell2Rho |
ParticlePar5 //rho for shell 2 |
|
RectParallepid |
particle size |
Is side a |
Side B ratio |
ParticlePar1 //Ratio side B/A |
|
Side C ratio |
ParticlePar2 //Ratio side C/A |
Structure factors & their parameters¶
Structure Fct |
Parameter |
ParticlePar |
|---|---|---|
Interferences |
ref |
Beaucage, G. (1995). J Appl Crystallogr 28, 717-728. |
Par1 |
ETA (center-to-center distance) |
|
Par2 |
Pack (number of particles In nearest neighbor sphere) |
|
Hard Spheres |
ref |
Percus-Yevick model, PERCUS,YEVICK PHYS. REV. 110 1 (1958), THIELE J. CHEM PHYS. 39 474 (1968), WERTHEIM PHYS. REV. LETT. 47 1462 (1981) |
Par1 |
Radius [A] (center-to-center distance between particles is 2*Par1) |
|
Par2 |
Volume fraction (fraction) |
|
Square Well |
ref |
SHARMA,SHARMA, PHYSICA 89A,(1977),212, NOTE - depths >1.5kT and volume fractions > 0.08 give UNPHYSICAL RESULTS when compared to Monte Carlo simulations |
Par1 |
Radius [A] |
|
Par2 |
Volume fraction (fraction) |
|
Par3 |
Well depth e/kT, dimensionless, positive values are attractive |
|
Par4 |
Well width, multiples of diameters |
|
Sticky hard sph. |
ref |
n/a in NIST macros |
Par1 |
Radius [A] |
|
Par2 |
Volume fraction (fraction) |
|
Par3 |
Perturbation parameter (0.1) |
|
Par4 |
Stickiness, tau |
|
Hayer Penfold MSA |
ref |
n/a in NIST macros |
Par1 |
Radius [A] |
|
Par2 |
Charges |
|
Par3 |
Volume fraction |
|
Par4 |
Temperature in Kelvin |
|
Par5 |
Monovalent salt concentration (M) |
|
Par6 |
dielectric constant of solvent |
|
Interprecipitate |
ref |
Formula 6 in APPLIED PHYSICS LETTERS 93, 161904 (2008) |
Par1 |
Distance L [A] |
|
Par2 |
Sigma (root-mean-square deviation (ordering factor)) |
|
DisorderedCrystal |
ref |
https://en.wikipedia.org/wiki/Structure_factor#Finite_crystals_with_disorder_of_the_second_kind |
Par1 |
Distance a [A] |
|
Par2 |
Sigma (root-mean-square deviation (ordering factor)) |
Important comment for Core-shell and Core shell cylinder (and Unified tube). The volume definition for Core-shell objects is matter of discussion. Heated at times and I suspect that the appropriate answer depends on the case when and how the FF is used. Therefore from version 2.26 Irena macros include option which needs to be set - both Core shell and Core shell cylinder will share common parameter (this parameter is global for all cases of calls to core shell form factors or their volumes) of volume definition. The options are: whole particle, core, and shell
Note: Unified tube is using as volume the volume of shell. It is how it is defined at this time and it is meant for cases like Carbon nanotubes, when this is appropriate. To match with core shell cylinder us “shell” as volume
Form Factor description¶
Spheroid¶
uses sphere form factor for aspect ratio between 0.99 and 1.01:
\(F^2(Q,R)=\frac{3(sin(QR)-(QR)cos(QR))}{(QR)^3}\)
volume \(V(R)=\frac{4\pi R^3}{3}\)
This calculation approximates integral over R as rectangle (compare with Integrated spheroid).
graph for R = 50A

For aspect rations smaller than 0.99 and larger than 1.01 uses standard form factor for spheroid:
F = Integral of (3/(QR^3))*(sin(QR)-(QR*cos(QR)))
where QR=Qvalue*radius*sqrt(1+(((AR^2)-1)*CosTh^2))
over of CosTh = 0 to 1. This is numerically calculated using 50 points (step in CosTh = 0.02). Following graphs are examples:
AR = 10
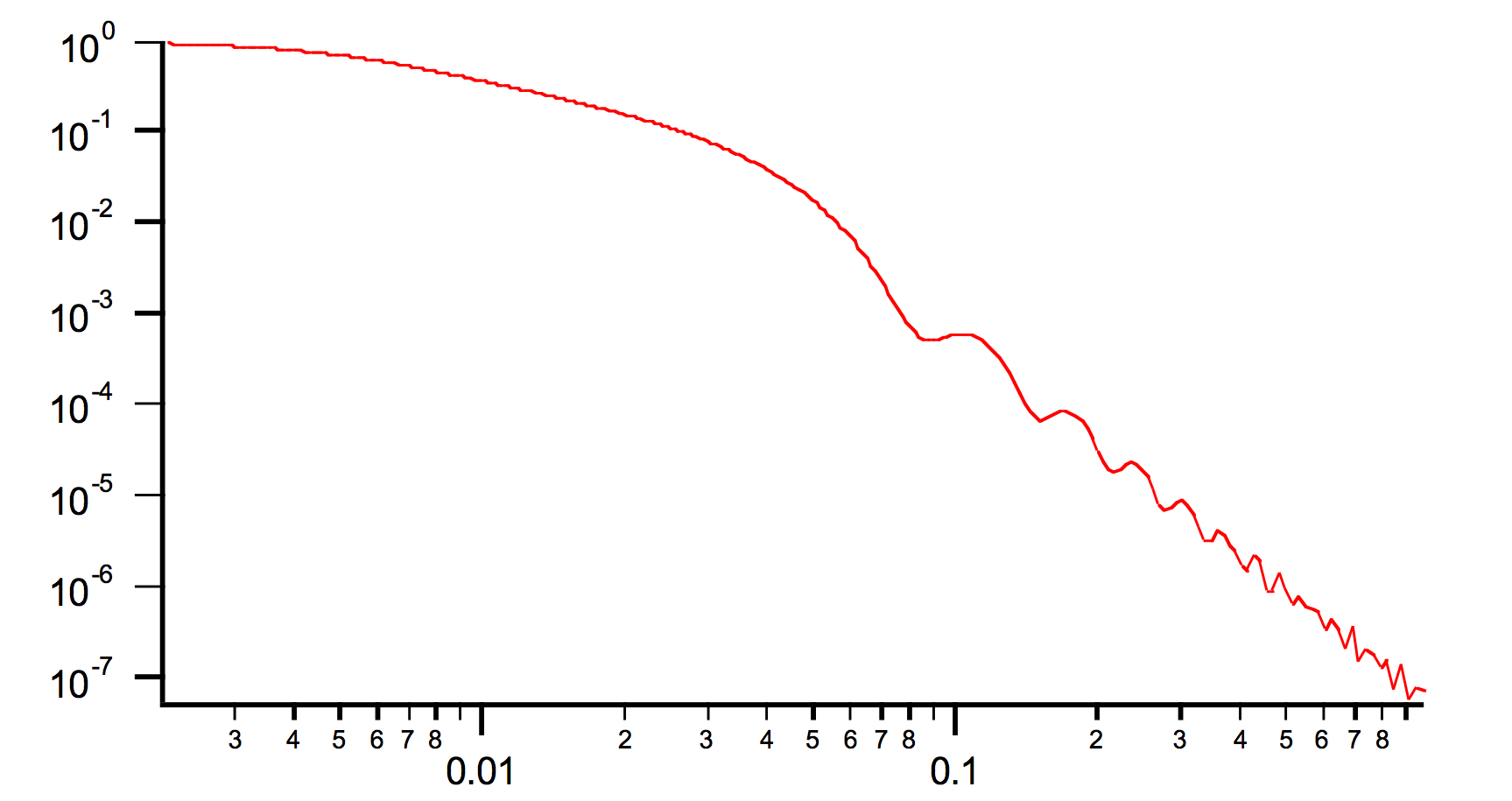
AR=0.1
Since Irena version 2.54 Spheroid with aspect ratio !=1 will use NIST xop to speed up its calculations.
Integrated_Spheroid¶
same code as in the spheroid, but in this case the code integrates over the width of the R bin. Note, the bin star and end points are calculated linearly (even for log-binned data) as half way distance:
Rstart = (Rn + Rn-1)/2Rend = (Rn + Rn+1)/2Uses adaptive steps to integrate Bessel function oscillations of the form factor over the width of the bin in R - note, the averaging is done including the volume of particles involved. This code is quite convoluted and time consuming. Its only reasonable use is for cases with wide bins in radius (R), when this removes some of the Bessel function oscillations.
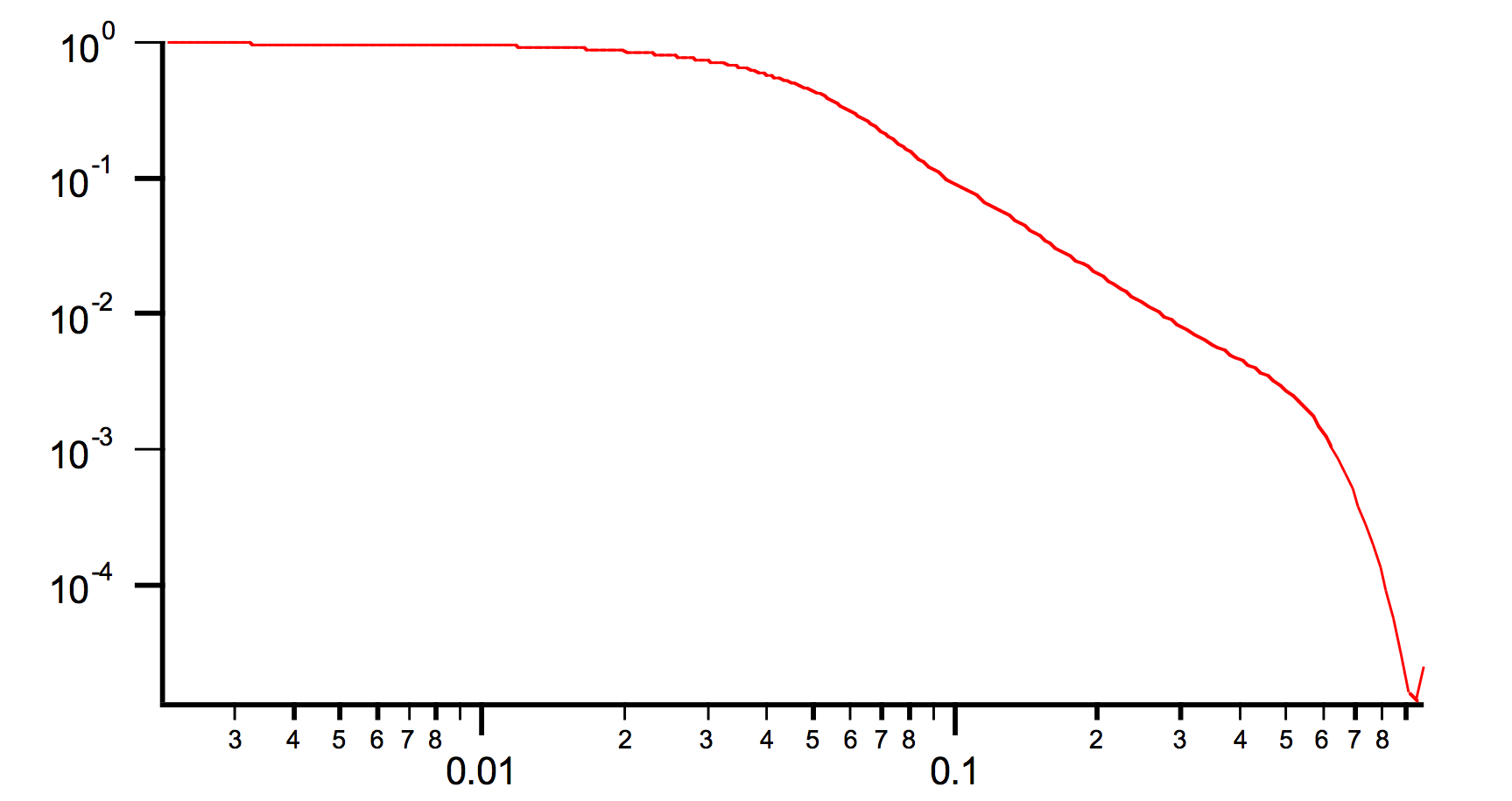
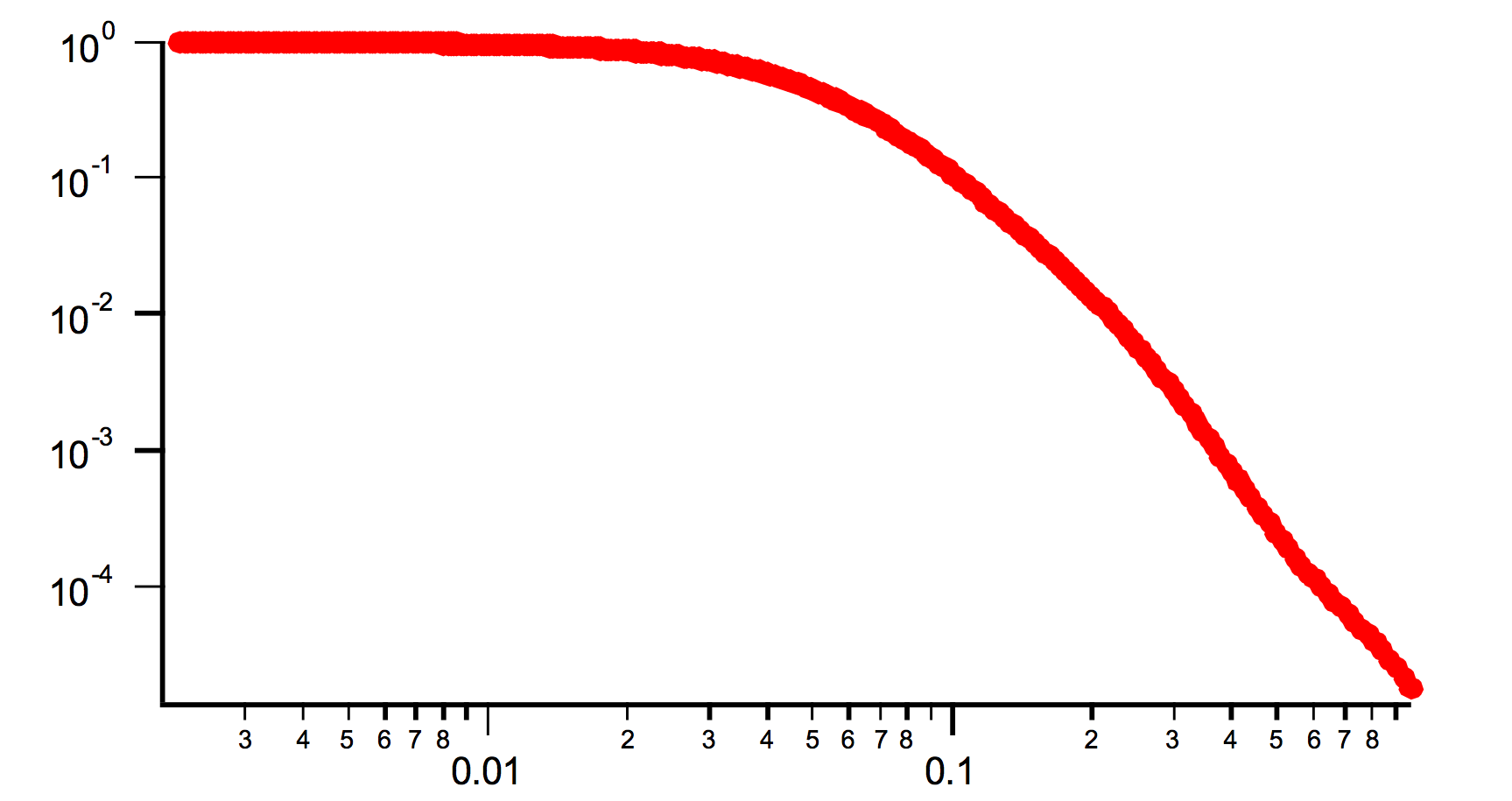
Examples with R width 40A, average size 50A (that means R varies from 30 to 70A). Note that the Bessel function oscillations are somehow smooth out. With wider bins in R these oscillations may disappear all together.
AR = 1 (sphere)
AR=10 (Spheroid)
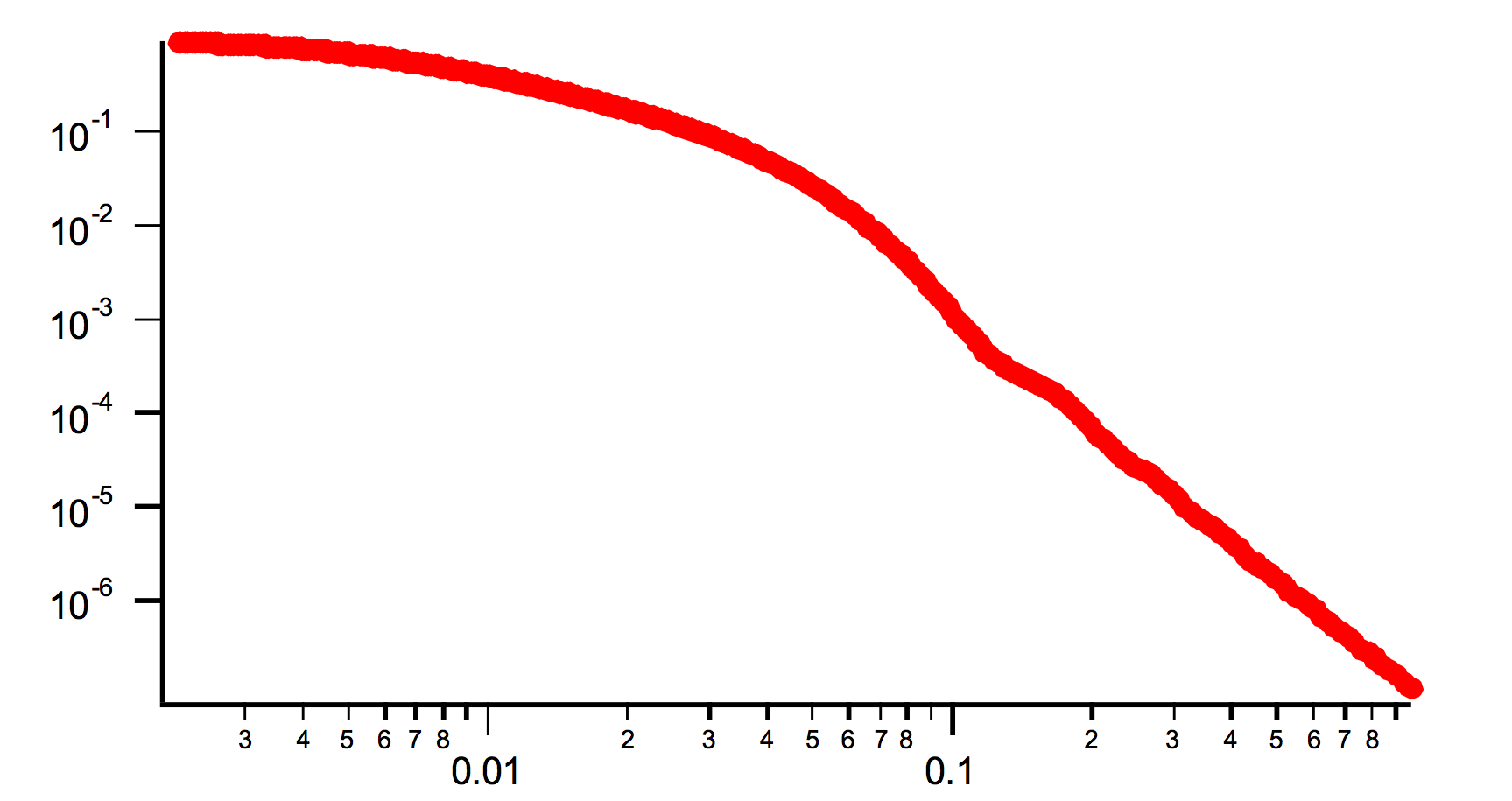
AR=0.1 (spheroid)
Cylinder, Disk, and CylinderAR¶
- The code uses the following code to calculate form factor for cylinder. Note, that also this code is doing the same integration as integrated spheroid above (see 2). There are three variants available:
- Cylinder “size” is radius. User needs to define length, which can be fitted, but no size distribution. Length can be smaller (thickness) or larger (length) than radius, making this disk or cylinder.Disk “size” is thickness. User needs to define radius, which can be fitted, but no size distribution. Most likely radius>thickness.CylinderAR has fixed aspect ratio, which can be fitted. Therefore the same size distribution is applied to both radius and length/thickness.
Form factor = integral over (Ft) for Alpha = 0 to pi/2, Ft is below:
LargeBes=sin(0.5*Qvalue*length*Cos(Alpha)) / LargeBesArg
SmallBessDivided=BessJ(1, Qvalue*radius*Sin(Alpha))/Qvalue*radius*Sin(Alpha)
Ft = LargeBes*SmallBessDivided
Examples Cylinder with length 500A and radius 50A.
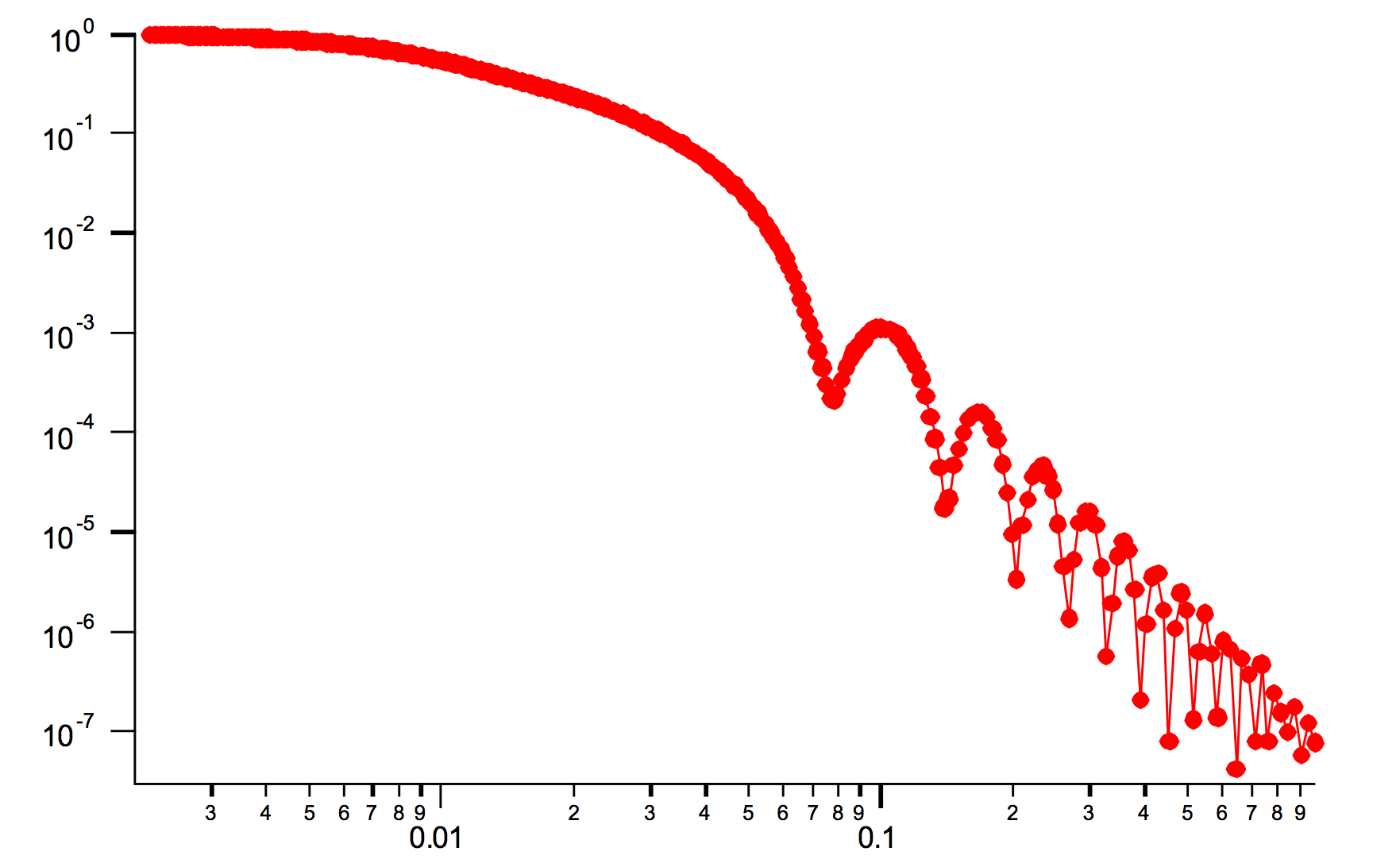
Disk (cylinder) with radius 500A and length 50A.
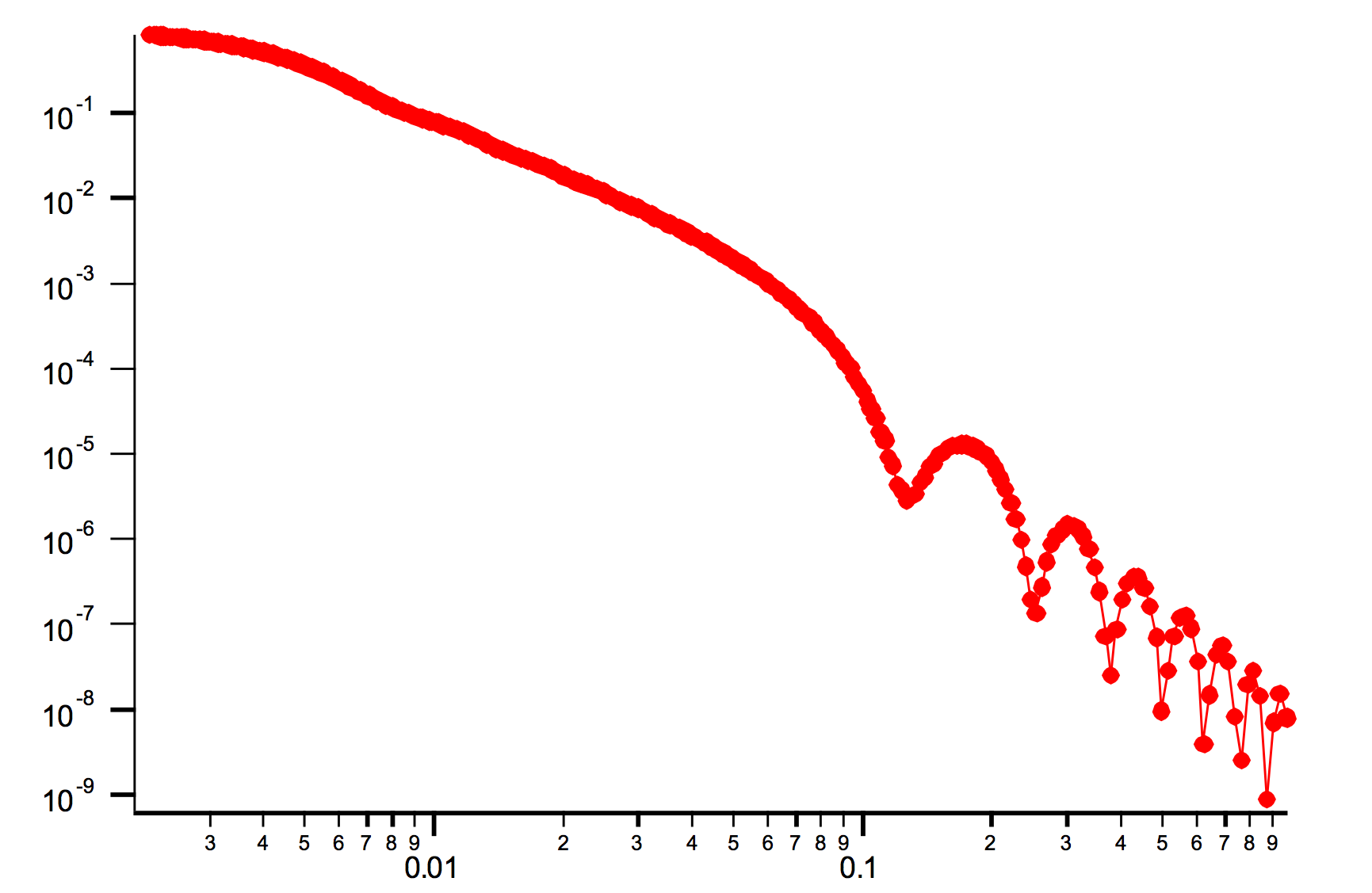
Since Irena version 2.54 Cylinders will use NIST xop to speed up its calculations. If the xop is not available, Igor will use all available cores to speed up the calculations.
CoreShell¶
One thing to remember: the total radius of this particle is core radius + shell thickness… If you use diameter as dimension of the particle (new in Irena version 2.53), the total diameter of the particle is diameter+2*shell thickness. Note, this form factor calculation also includes integration over the width of bin in radii (same as integrated spheroid and cylinder).
Note: Input form factor parameter for core/shell/solvent is rho in [1010 cm-2] - this is very important to keep in mind.
Note, that there is volume definition choice you need to do: Whole particle, core, or shell, as appropriate for given problem. This volume definition is used for all volume calculations for this particle. It is global parameter for all core shell cylinder or core shell calls in the WHOLE EXPERIMENTÅc.
Code (heavily simplified!):
\(\Delta\rho=\rho_{core} - \rho_{shell}\)
//core
\(Result_{core}(Q,R)=\frac{3(sin(QR)-QRcos(QR))}{(QR)^3} - \Delta\rho \frac{4\pi R^3}{3}\)
//Now add the shell (skin) , thickness is called Rshell
\(r = R+R_{shell}\) this is radius of the core+shell
\(\Delta\rho=\rho_{shell} - \rho_{solvent}\)
\(Result_{shell}(Q,r)=\frac{3(sin(Qr)-Qrcos(Qr))}{(Qr)^3} - \Delta\rho \frac{4\pi r^3}{3}\)
//summ them together and normalize by the total particle volume
\(F^2(Q,R,r)=\frac{(Result_{core}(Q,R) + Result_{shell}(Q,r))^2}{V_{i}(R,r)}\)
Volume definition depends on the setting of global parameter described in Core-shell form factor and is either:
Whole particle volume
\(V_{i}(r)=\frac{4\pi (R+r)^3}{3}\)
Core volume
\(V_{i}(r)=\frac{4\pi R^3}{3}\)
Shell volume
\(V_{i}(r)=\frac{4\pi (R+r)^3}{3} - \frac{4\pi R^3}{3}\)
Make sure your choice of volume formula is appropriate, especially if you want to do absolute calibrated calculations.
Note, that to my surprise these calculations (copied from NIST Form factors) do not normalize correctly to 1 at low q. The reason is that the weighting is done by volume and contrast. I’ll need to look into this again and in detail…
Example, Radius 50A, skin thickness 10A, contrast ratio 0.6

CoreShellPrecipitate¶
This is unique form factor, which - even for dilute system - results in “diffraction peak” type scattering. It is a very special case, when core shell particle is formed from matrix and as it is formed, the core chemistry/rho deviates from matrix chemistry/rho. If the diffusion in the matrix is not fast enough, the chemistry around the particle changes, which results in rho changing in the other direction. Therefore one can end with core shell particle which has higher-then-solvent rho core surrounded by lower-then-solvent rho shell (or the other way). With average rho same as matrix. In such case at low-qs the particle “disappears” since we are probing material on larger length scales, and on average at those length scales the rho is the same. Fro example of this type of precipitation see:
Imhoff, S.D., et al., Kinetic transition in the growth of Al nanocrystals in Al-Sm alloys. Journal of Applied Physics, 2012. 111(6): p. 063525-9.
Remember, that by basic nature of this logic, the rho of the core/shell needs to be one larger and the other smaller than solvent rho. Also, they probably need to be pretty close together. If this is not correct, the code would create negative shell thicknesses and abort. Do not do it, it is not very physical…
The particle volume is always volume of the core. I think no other logic makes too much sense.
Code uses regular core shell form factor (see above). For each size the shell thickness is calculated so the average rho of the particle matches the rho of the solvent. First we calculate:
\(ShellVolume=\frac{CoreVolume(SolventRho - CoreRho)}{ShellRho - SolventRho}\) Then we calculate the shell thickness for known ShellVolume and known core radius.
Core volume = \(\frac{4}{3} \pi R^3\)
Example, Radius 50A, Core Rho 110, Shell Rho 85, Solvent Rho 90; note, this internally resolves to shell thickness of 35.5A.
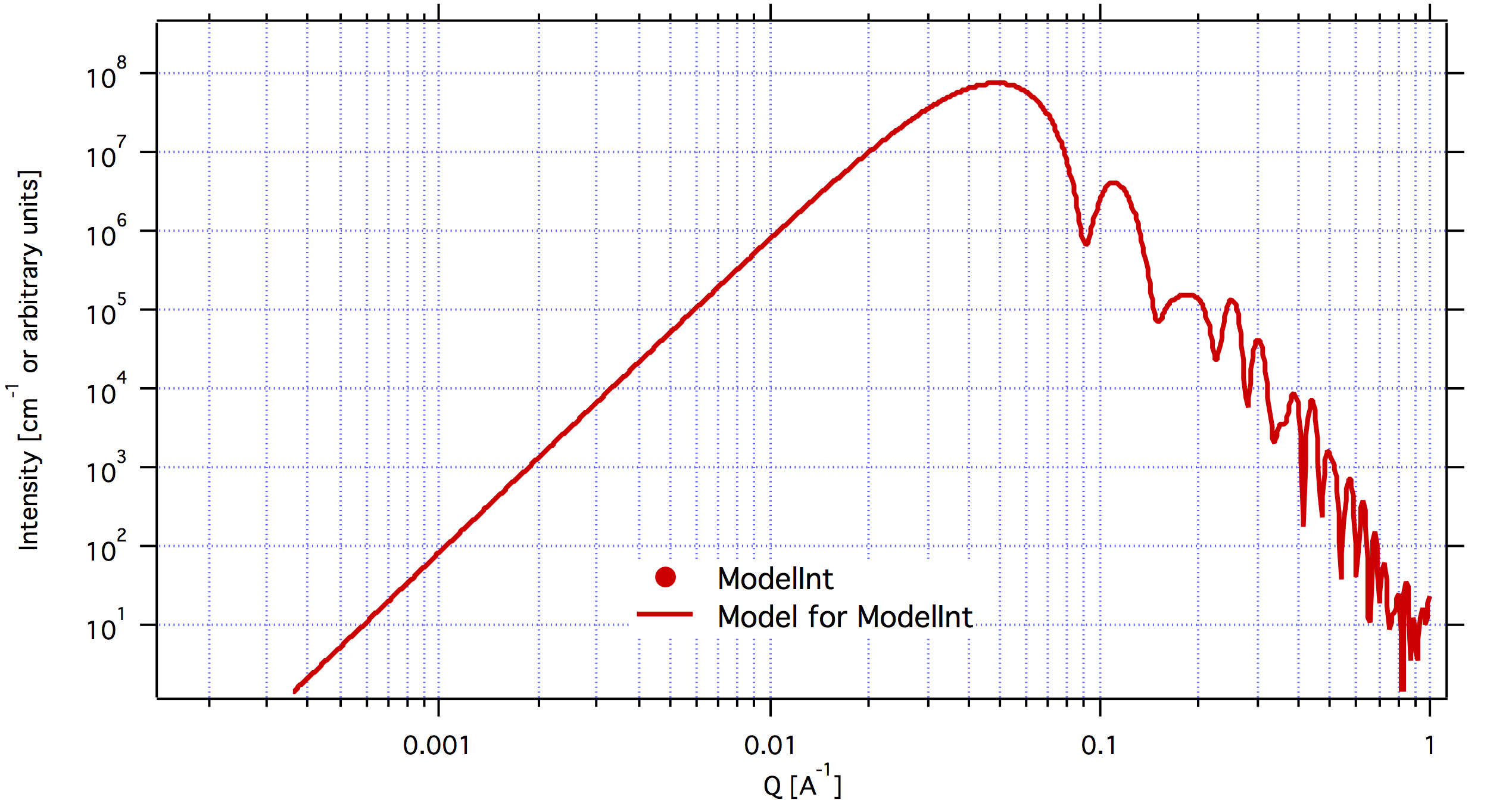
CoreShell Cylinder¶
Note, this form factor calculation also includes integration over the width of bin in radii (same as integrated spheroid and cylinder).
This code has been developed some time ago and I am not sure about it’s function…
Code which is being used is direct copy of NIST Core shell cylinder.
Note, that there is volume definition choice you need to do: Whole particle, core, or shell, as appropriate for given problem. This volume definition is used for all volume calculations for this particle. It is global parameter for all core shell cylinder or core shell calls in the WHOLE EXPERIMENTÅc.
Volume definition depends on the setting of above discussed global parameter and is either: Whole particle volume = \(\pi*(R+r)^2*(L+2r)\)
Core volume = \(\pi R^2L\)
Shell volume = \(\pi*(R+r)^2*(L+2r) - \pi R^2L\)
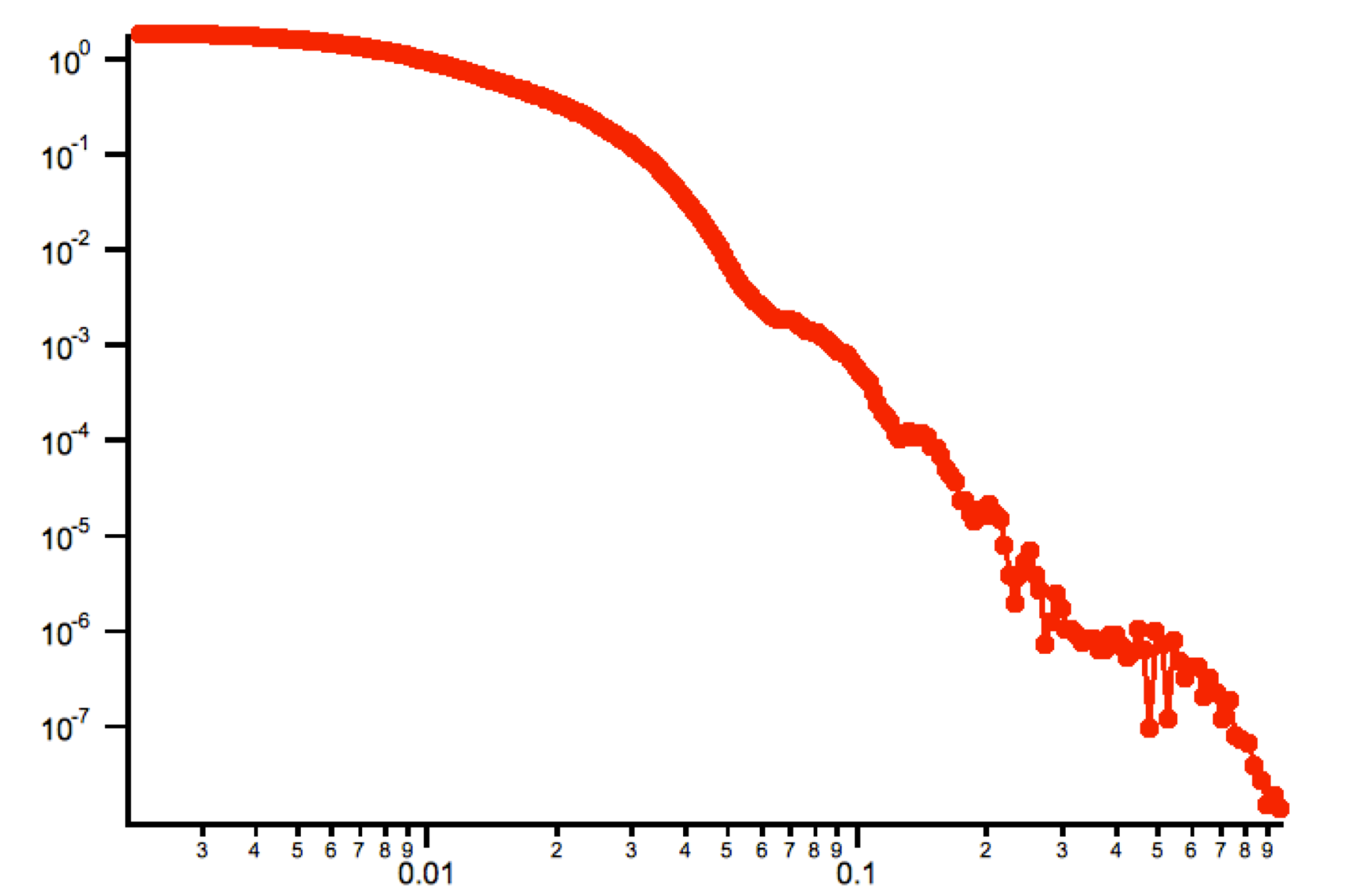
Fractal Aggregate¶
This form factor was requested by Dale Schaefer and I cannot very well guarantee its functionality….
code:
where:
Note, that parameters are : Param1 - radius of primary particle param2 - fractal dimension of the fractal particles
Example for R=100A, radius of primary particle 10 A and fractal dimension 2.5.

Comment: Note, that this is not scaled correctly at all… I have no idea why - apparently this formula is either wrongly coded or plainly does not behave right.
CoreShellShell¶
This form factor has been provided by Fan Zhang, many thanks to him. Description of the model:
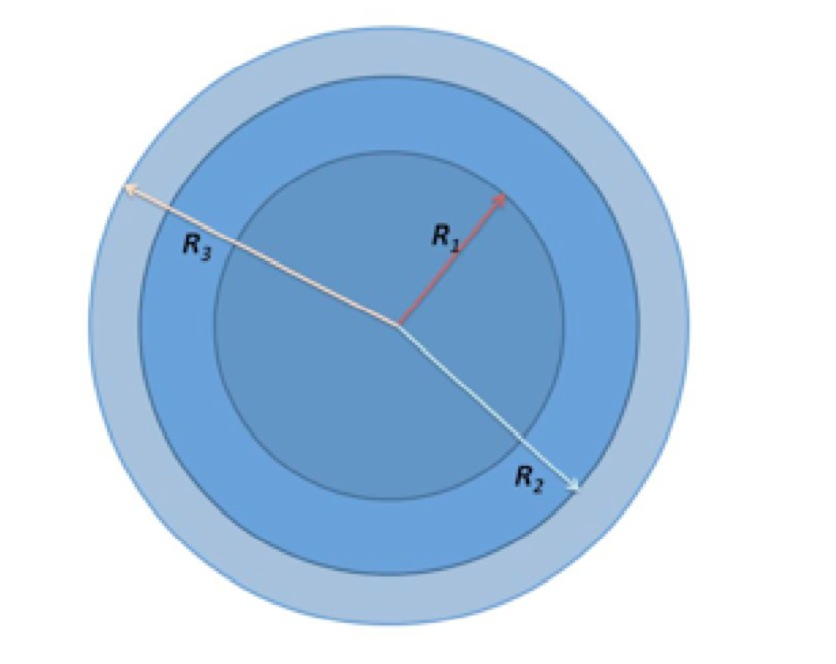
Scattering Length Density Rho:
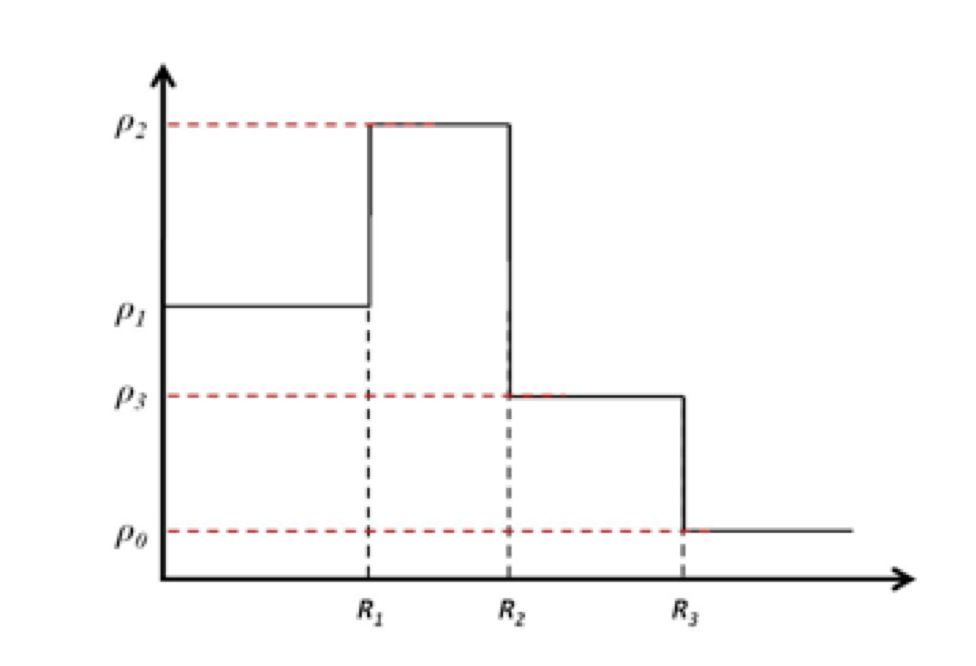
List of Model Parameters (used in formulas):
R1 : core radius
R2 : outer radius of the first shell
R3 : outer radius of the second shell
\(\rho_{0}\) : scattering length density of the matrix
\(\rho_{1}\) : scattering length density of the core
\(\rho_{2}\) : scattering length density of the first shell
\(\rho_{3}\) : scattering length density of the second shell
First-order Bessel function of the first kind is defined as
Volume is defined as
Form factor of the core-shell-shell structure is:
NOTE – GUI panel input parameters – NOTE¶
Input parameters in the GUI panel are NOT \(R_{2}\) or \(R_{3}\) for the shells, but are thicknesses of those shells. This is to make the GUI understandable and compatible with selection of the use of radii or diameter for “size”. So, in this case we have:
“particle size” = \(R_{1}\) - this is the dimension of the particle as defined by Modeling package. This is what your Mean size reflects.
“Shell 1 thickness” = \(R_{2}\) - \(R_{1}\), this is thickness of the shell 1 in [A].
“Shell 2 thickness” = \(R_{3}\) - \(R_{2}\), this is thickness of the shell 2 in [A].
Volume definition depends on the setting of global parameter described in Core-shell form factor and is either:
Whole particle
\(V_{i}(r)=\frac{4\pi (R+r)^3}{3}\)
Core volume
\(V_{i}(r)=\frac{4\pi R^3}{3}\)
Shell volume
\(V_{i}(r)=\frac{4\pi (R+r)^3}{3} - \frac{4\pi R^3}{3}\)
Where shell thickness “r” is sum of the two shell thicknesses form GUI (in A), i.e., \(r = R_{3}-R_{1}\) in the graph above. Make sure your choice of volume formula is appropriate, especially if you want to do absolute calibrated calculations.
SphereWHSLocMonoSq¶
This is form factor combined with structure factor – Based on Jan Skov Pedersen J. Appl. Cryst paper : J. Appl. Cryst. (1994) 27, 595-608. The model is locally mono dispersed system, therefore locally one can use spheres Form factor combined with structure factor. For each bin here the code calculates F(Q,R)^2 * S(Q,D,phi), where D ~ R via input parameter. Phi is simply fraction of Percus Yevic structure factor.
The result is different than multiplying dilute system by Structure factor – that assumes that the distance for Structure factor is the same for all sizes. In this case the ratio of distance to size of particle is the same. We assume here that the phi is the same for all sizes.
Suffise to say, that using this form factor with another structure factor is meaningless and garbage will be produced.
Janus CoreShell Micelle¶
This is form factor based on manuscript: T. Futterer, G. A. Vliegenthart, and P. R. Lang, “Particle Scattering Factor of janus Micelles”, Macromolecules 2004, 37, 8407-8413. The Form factor follows formula 3 of this manuscript
which describes scattering from the particle on the left of the Image 1 from their manuscript (below).

Example of results:
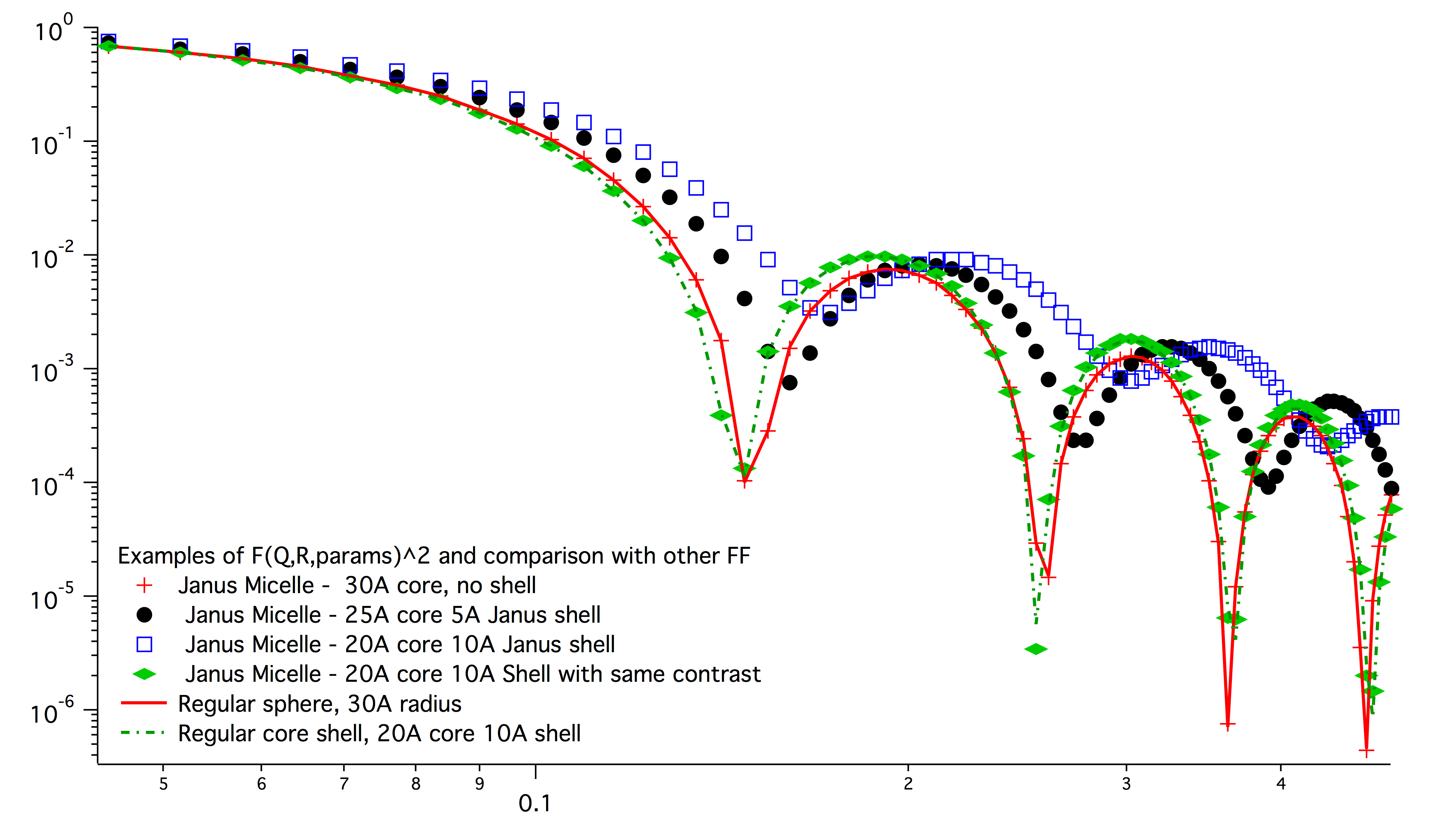
Note: the results in the above graph are scaled to F^2(Q=0) = 1. Since the formula included scattering length densities, normalization by the volume does not result in F^2(Q=0) = 1. This may result in unexpected problems with absolute calibration.
This FF is implemented twice…
The reason for the two implementations is, that in usual implementation the shell thickness is fixed while the particle size has size distribution - but this is possible ONlY if core has distribution of sizes. This may be incorrect, as someone can have monodispersed cores, but distribution of shell thicknesses.
Note, that the “Janus CoreShell Micelle 2 and 3” will not work with some of the tools in Irena as all assume size represents total size (core+shell). Be warned, results will be difficult to present meaningfully! You are on your own…
Janus CoreShell Micelle 1: Mean radius 40A, width 0.3A (Gauss), Shell thickness 10A,
Janus CoreShell Micelle 2: Core radius 30A, Mean radius 40A, width 0.3A (Gauss) :
Janus CoreShell Micelle 1: Pseudo sphere (shell thickness = 0), Radius = 40 A,
Real sphere, contrast 14903.5 (Au-water):

Note the suspicious difference in calibrations. See note above about my suspicion on the problem here…
Real core shell system (pick shell contrast 34.95). Use “Whole particle” as volume.
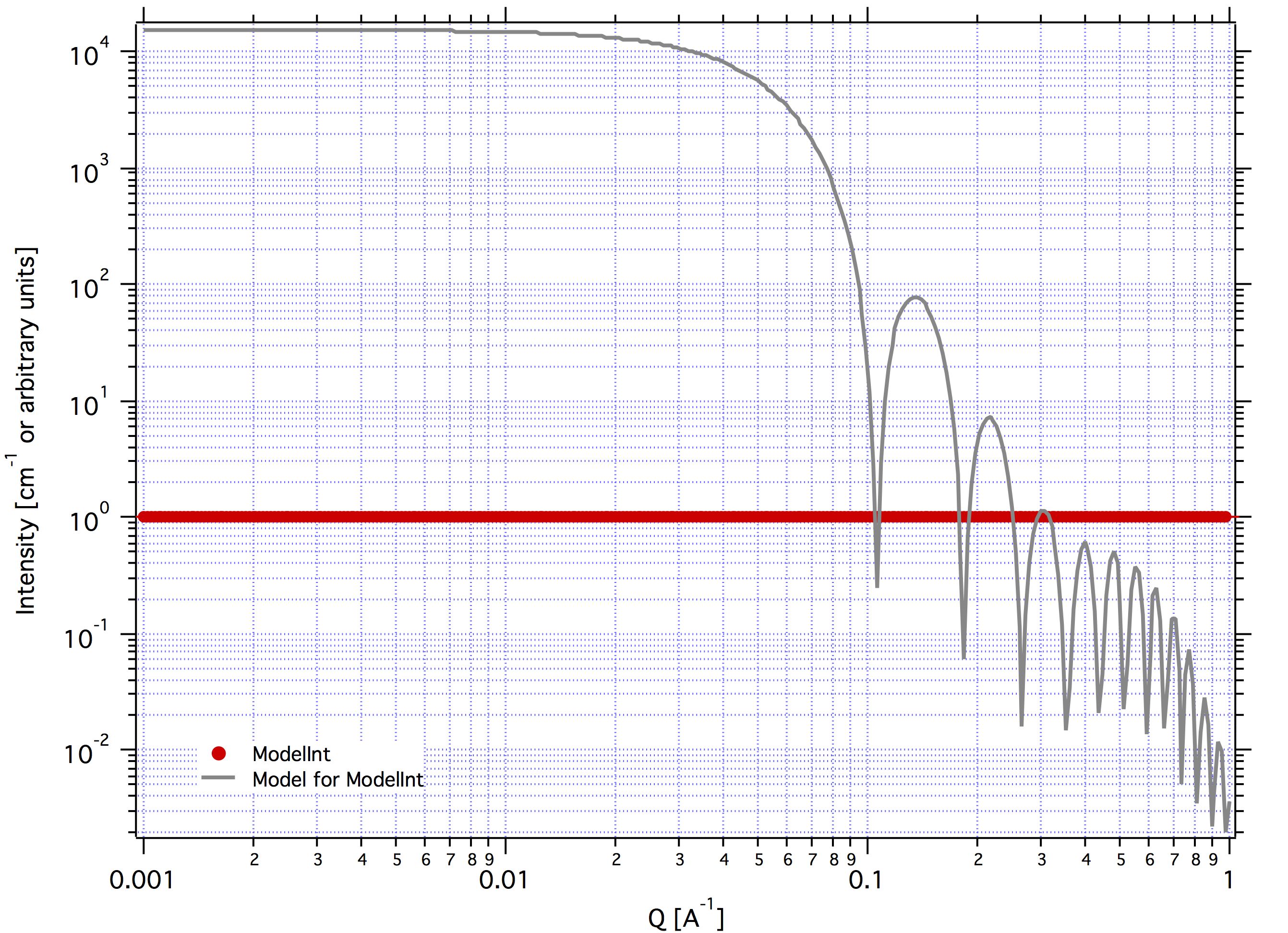
Janus CoreShell Micelle 1, fake the core shell with same contrast (34.95) for both shells. Recall that the total size of the CoreShell in Irena is radius of core (“Radius”)+ shell thickness; while for Janus CoreShell Micelle 1 it is just Radius (see image).
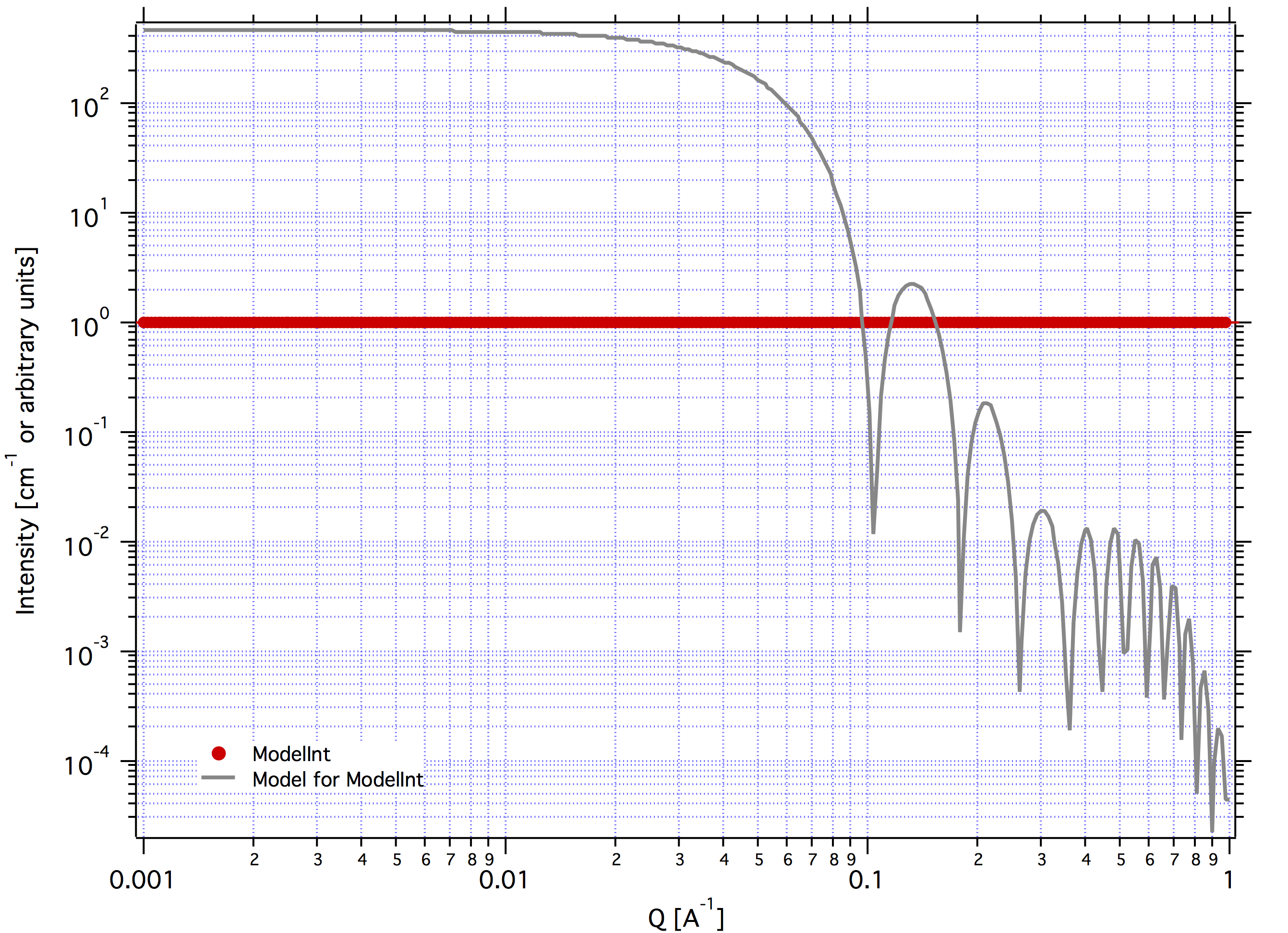
The difference in absolute intensity here is surely related to different assumptions on volume of particle.
RectParallelepiped¶
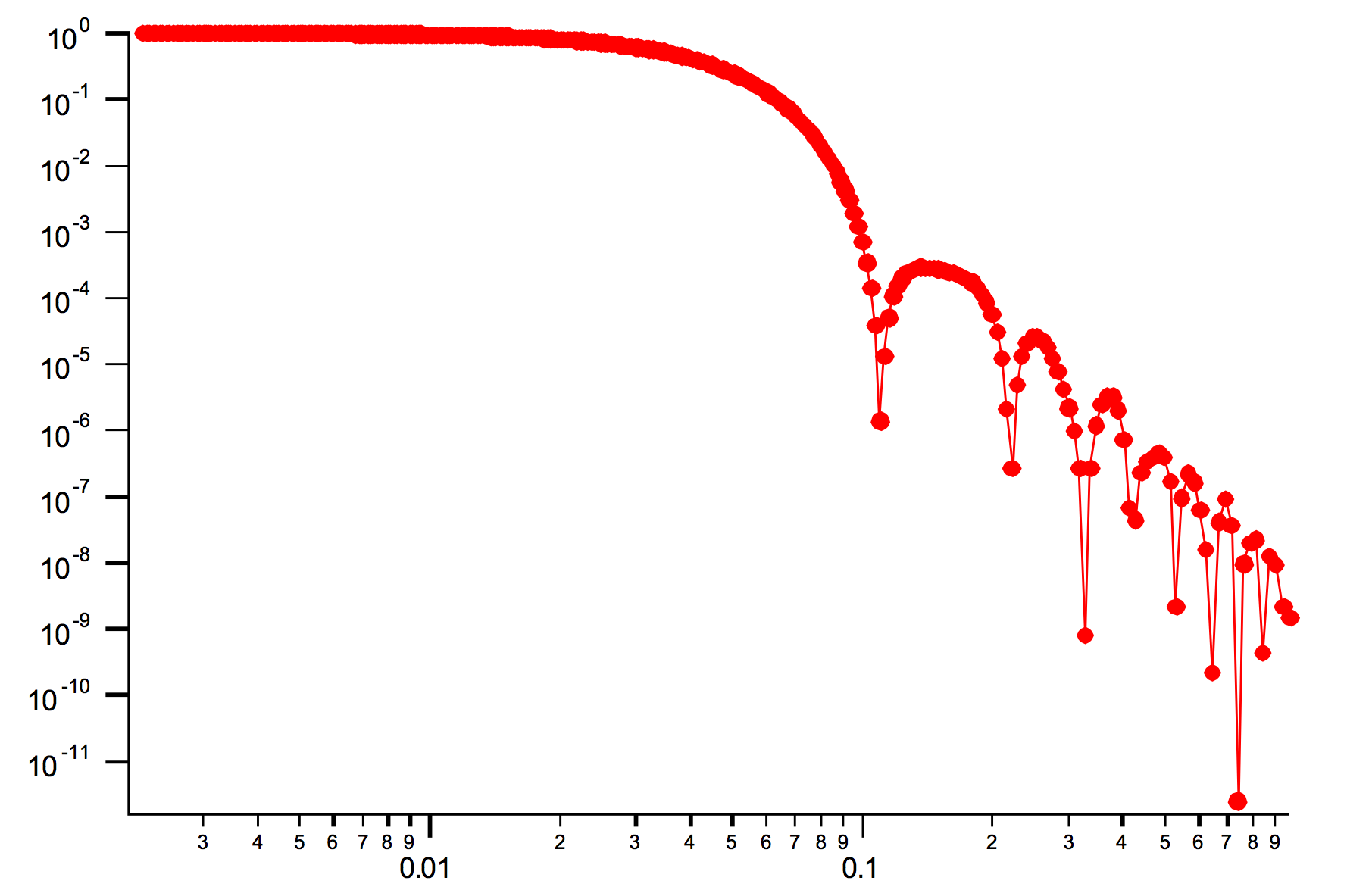
This is form factor or rectangular Parallelpiped, cuboid shape with side A x B x C and all angle 90 degrees. This form factor is ONLY available if NIST form factor xop is installed on the computer. If you install NIST SANS package http://www.ncnr.nist.gov/programs/sans/data/red_anal.html it installs xop which provides fast calculations of the various form factors. Since version 2.53 Irena will take advantage of some of these form factors. In the case of rectangular Parallelpiped see NIST form factor description. It seems they had to go to original manuscript and recreate the form factor from the German original, Mittelbach and Porod, Acta Phys. Austriaca 14 (1961) 185-211, equations (1), (13), and (14) (in German!). Most publications citing this form factor seem to be wrong (I think there is error in Pedersen 1997 manuscript I was working with, Steven cites other manuscripts which seem to have bugs in them).
If you use this form factor, cite Steven Kline manuscript for NIST package: “Reduction and Analysis of SANS and USANS Data using Igor Pro”, Kline, S. R. J Appl. Cryst. 39(6), 895 (2006).
Here is example of Form factor
Cuboid, 60A sides:
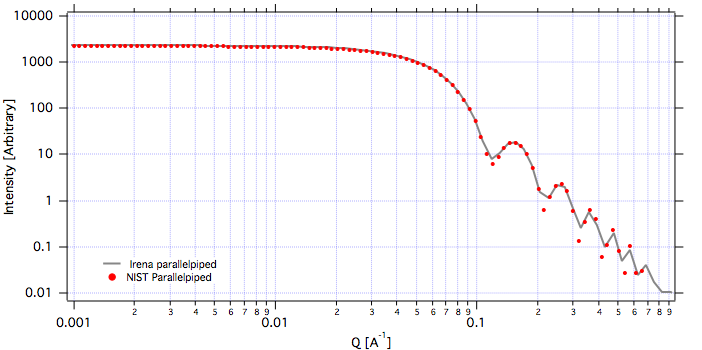
Hereis Parallelepiped with sides 60A, 120A, 180A:
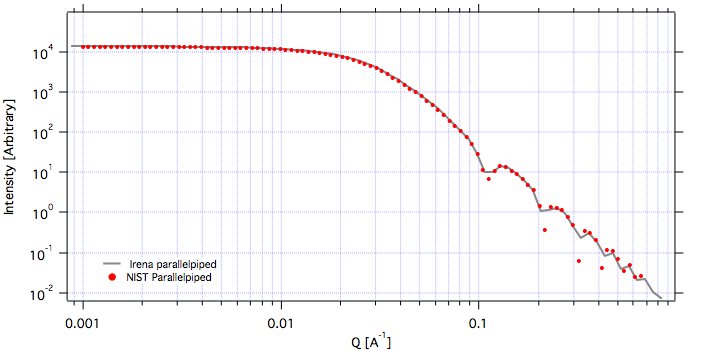
Note, Irena assumed some size distribution (narrow, but some) while NIST package, assumes monodispersed particle. Therefore the differences in oscillations.
User Form Factor¶
is flexible option to use when Irena does not have the specific form factor a user need. It uses user provided functions for Form factor and Volume of a scatterer. User provided functions need to be in the form of:
F(q,R,par1,par2,par3,par4,par5) = Form factor itself
V(R,par1,par2,par3,par4,par5) = Volume of particle function
the names for these need to be provided in strings, the input of these function is q [1/A] and R [A]. These function must declare the 5 parameters, but they are not required to use them internally, when not needed. Graphical interface for the controls of the User Form Factor opens when User form factor is selected (or reselected if needed). The GUI opens together with text document describing how to use and some demo functions:
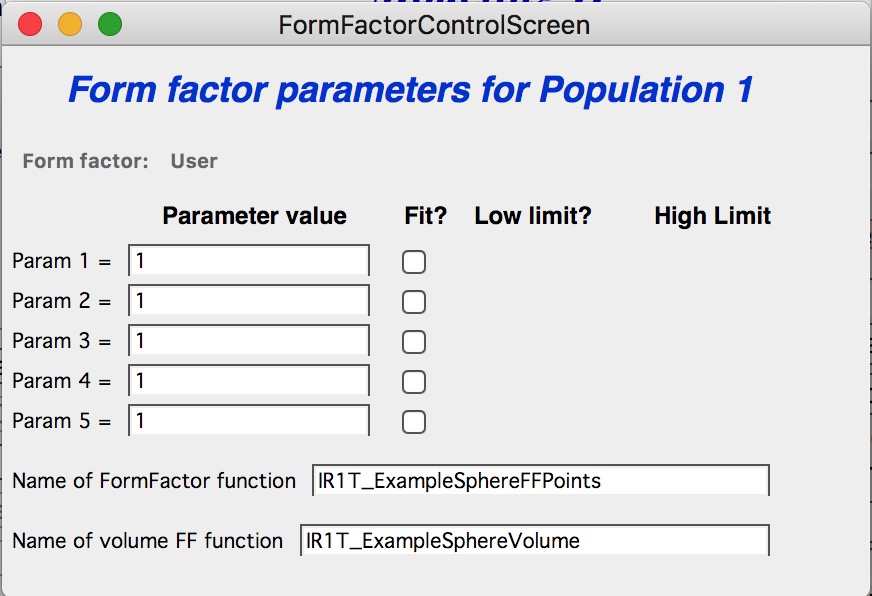

Github Irena depository has place where users can share their form factors. Instructions how to download are on this page. If you have Form factor to share, please, send it to ilavsky@aps.anl.gov.
Example of these functions for sphere:¶
Testing and using Form factors in users own code¶
To verify that the form factor works for you and to use the form factor if your own functions use following process and functions:
Generate Q wave with Qs for which the data are to be calculated
Generate intensity wave (will be redimensioned as necessary, so the only thing is, it should be double precision).
Generate distribution of radii wave - if you want to use single R, create wave with single point
decide what you want to calculate:
5. Run following command: IR1T_GenerateGMatrix(R_FF,Q_wave,R_dist,powerFct,”form factor name”,param1,param2,param3,param4,param5, “”, “”)
This function will return R_intensity, which is generally matrix with dimensions numpoints(Q_vector) x numpoints(R_dist), if R_dist has 1 point only, returned is wave (vector) as expected and reasonable… The param1 - param5 are form factor parameters, as desribed in chapter 1, the “” at the end are for user form factor functions (there go the strings with names of user form factor and volume function). “form factor name” is name from list in chapter 1.
Create log-log plot of the data if R_dist has single point. If R_dist has more point, well, you have to pull out the right column of data you need to plot.
Note, that if the IR1T_GenerateGMatrix function returns wave of NaN values if unknown name of form factor is passed in.
or
Display R_FF vs Q_wave
- ModifyGraph log=1
//creates log-log graph of
Structure factors description¶
This is list of library of structure factors. These structure factors enable to deal with limited S(Q) effects in Irena package. The functionality is provided by library, which can be called by any other user code. The library provides also GUI for setting the user parameters. In principle, further structure factors can be added if they have less than 5 parameters.
Interferences¶
This is original structure factor in Irena package. It has been provided as part of Unified fit model by Gregg Beaucage and is listed in his publication: Beaucage, G. (1995). Chapter 9 in ÅgHybrid Organic-Inorganic CompositesÅh, ACS symposium Series 585, edited by J. E. Mark, C. Y-C. Lee, and P. A. Bianconi, 207th National Meeting of the American Chemical Society, San Diego, CA, March 13-17, 1994. American Chemical Society, Washington, DC 1995. Pg. 97 – 111.
Note, that this model is, for most practical purposes, close to Hard spheres model with different definition of the parameters k (“Pack”) and \(\xi\) (“ETA”). Modeling extends the capabilities by including three more structure factors using code available from NIST Igor package (ref). Included are now: Hard spheres, Square Well, and Sticky Hard Spheres, which can be used in addition to interferences model above and no structure factor (dilute limit).
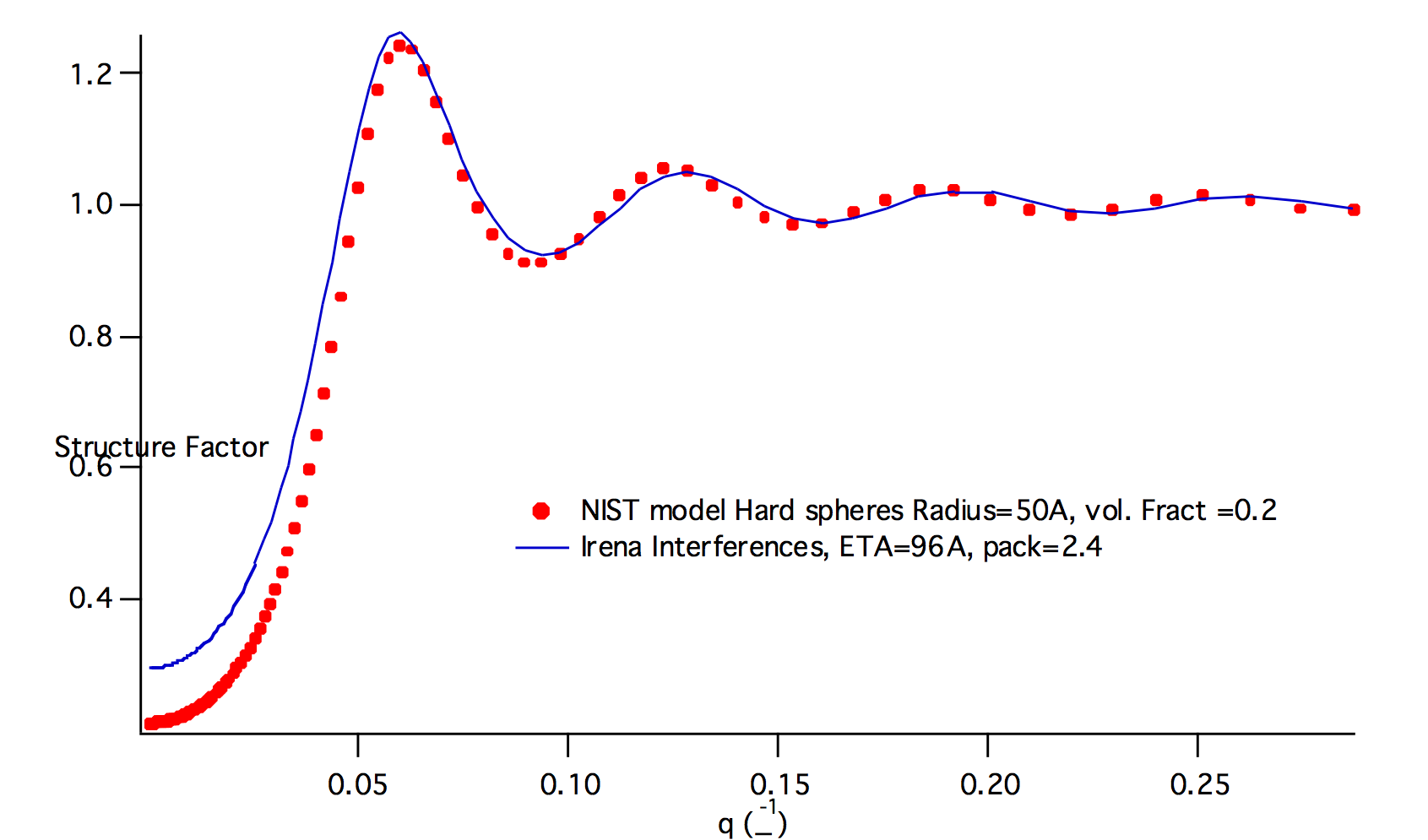
HardSpheres¶
The code for this structure factor has been copied from NIST SAS macros (Kline, S. R. (2006). J Appl Crystallogr 39, 895-900). Please, give them credit when using this structure factor. (http://www.ncnr.nist.gov/programs/sans/data/data_anal.html)
This is graph of NIST model and Irena implementation. Some info on HS parameters: The Radius is half distance between the centers of neighboring particles, so center-to-center distance is 2*RHS. The volume fraction is real Hard spheres volume fraction. If the sample is inhomogeneous, the volume fraction calculated from absolutely calibrated intensity of small angle scattering may be different (typically smaller) that structure factor volume fraction.
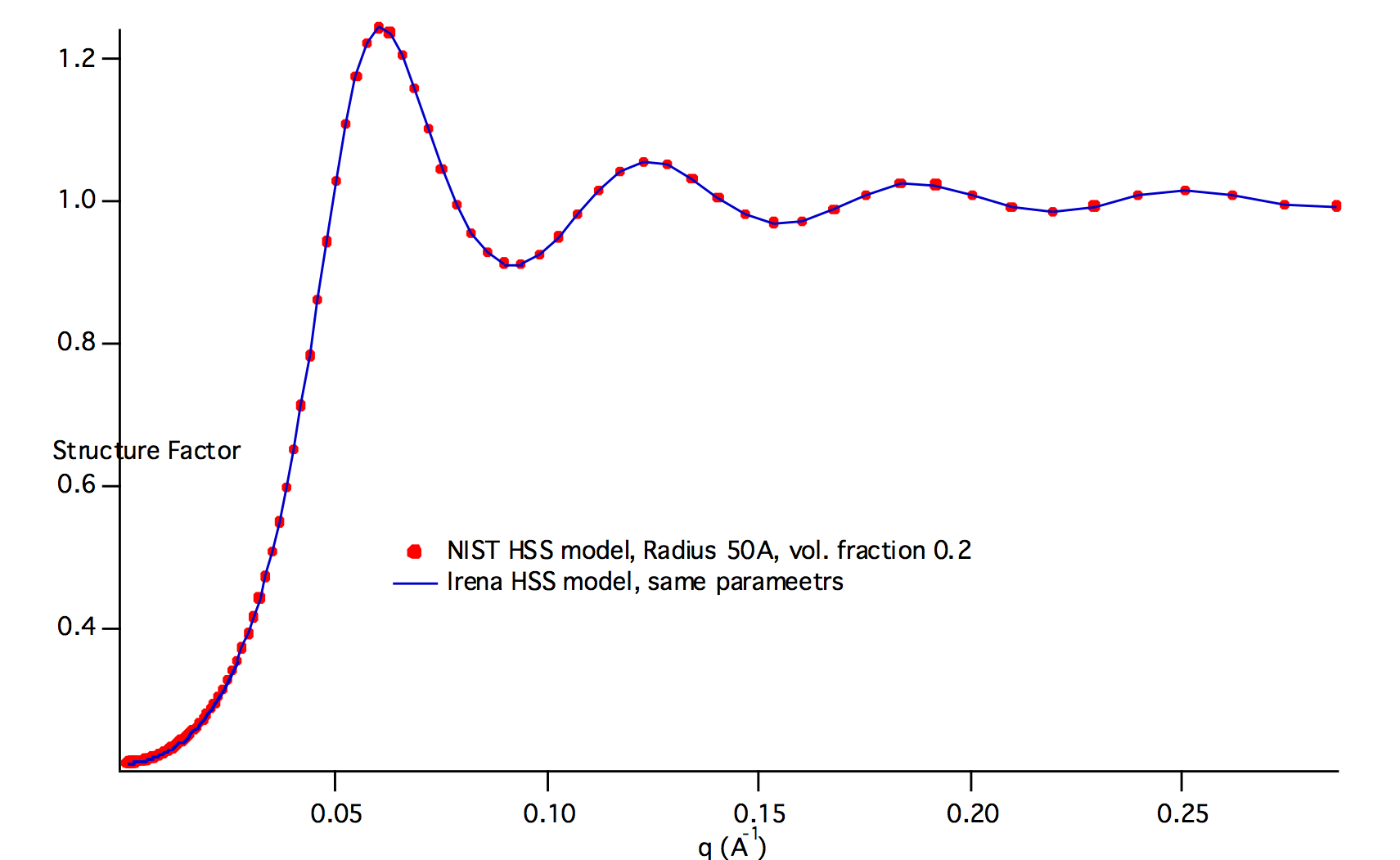
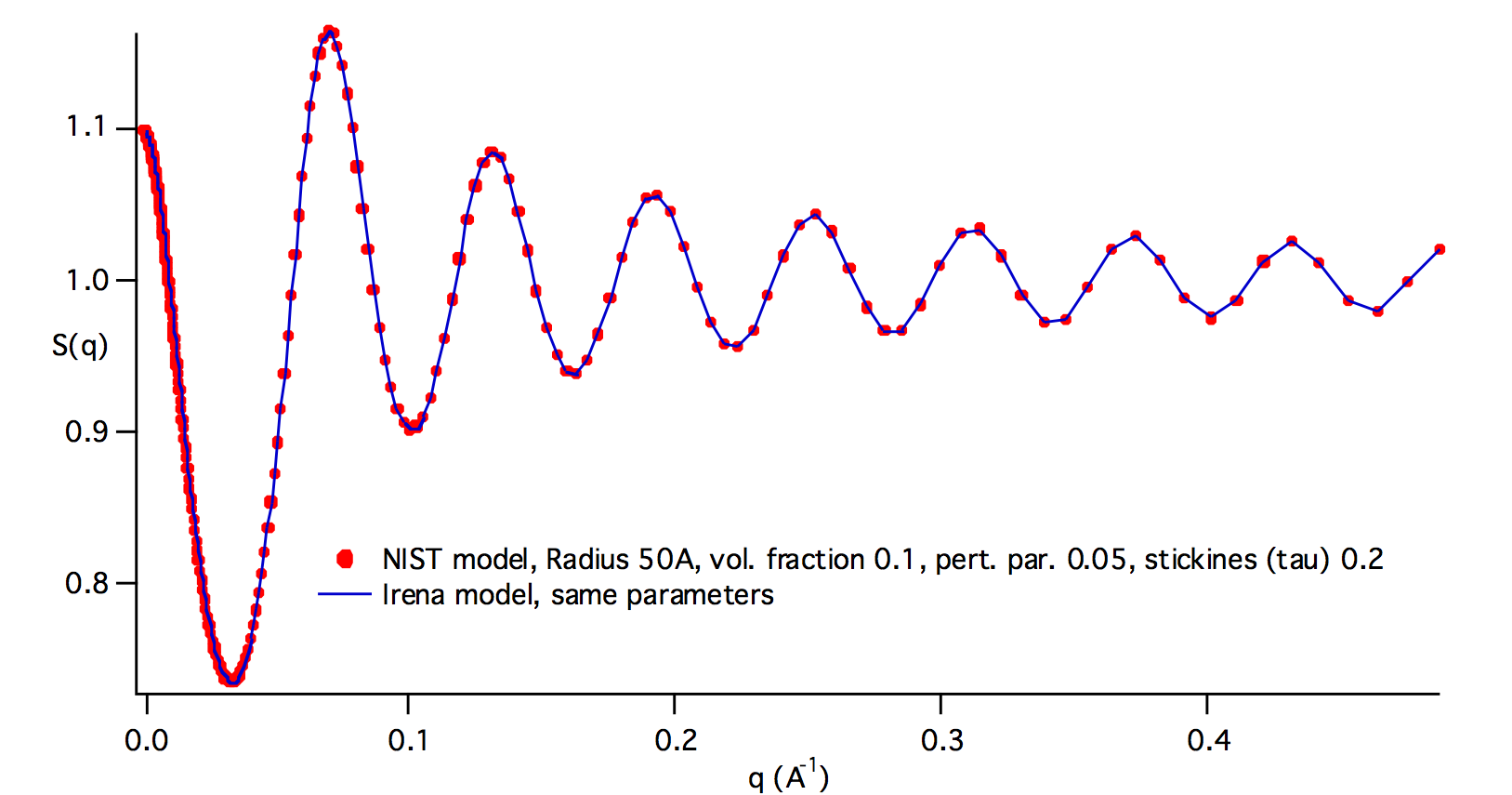
StickyHardSpheres¶
The code for this structure factor has been copied from NIST SAS macros (Kline, S. R. (2006). J Appl Crystallogr 39, 895-900). Please, give them credit when using this structure factor. (http://www.ncnr.nist.gov/programs/sans/data/data_anal.html)Åc
SquareWell¶
The code for this structure factor has been copied from NIST SAS macros (Kline, S. R. (2006). J Appl Crystallogr 39, 895-900). Please, give them credit when using this structure factor. (http://www.ncnr.nist.gov/programs/sans/data/data_anal.html)Åc
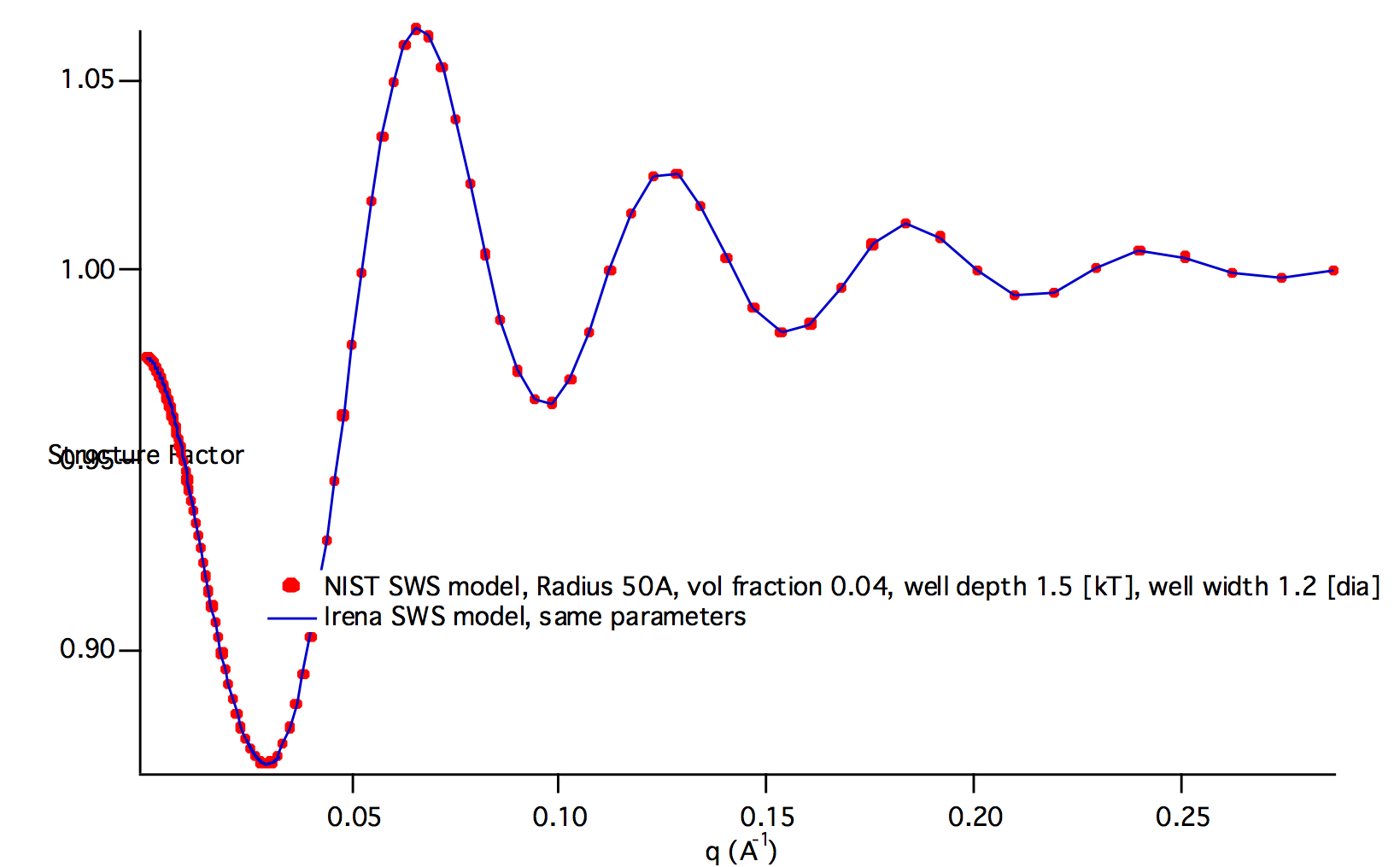
HayerPenfoldMSA¶
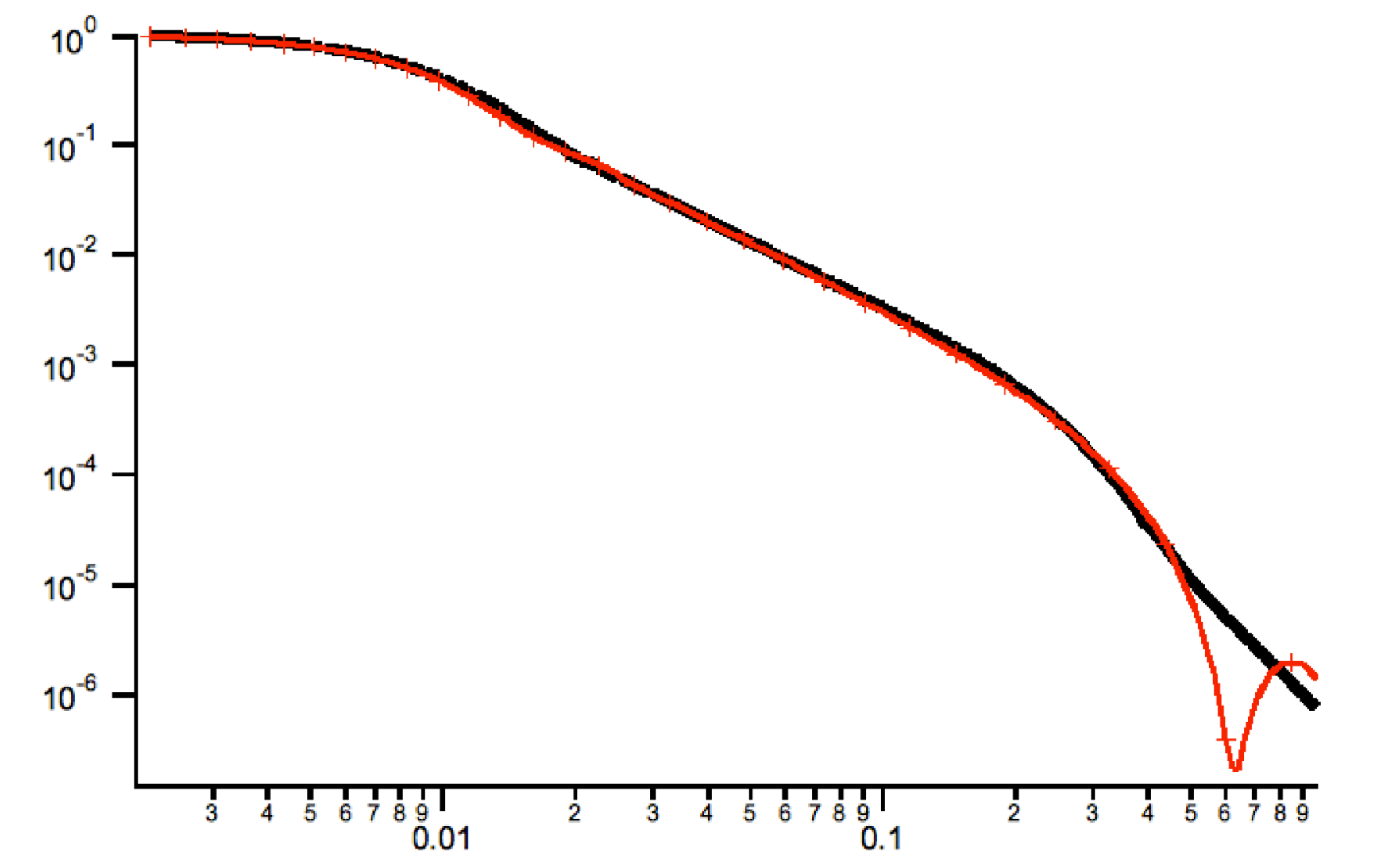
The code for this structure factor has been copied from NIST SAS macros (Kline, S. R. (2006). For any details on the use of these, please see the original code and description from NIST data analysis package (http://www.ncnr.nist.gov/programs/sans/data/data_anal.html)Åc Please, give them credit when using this structure factor.
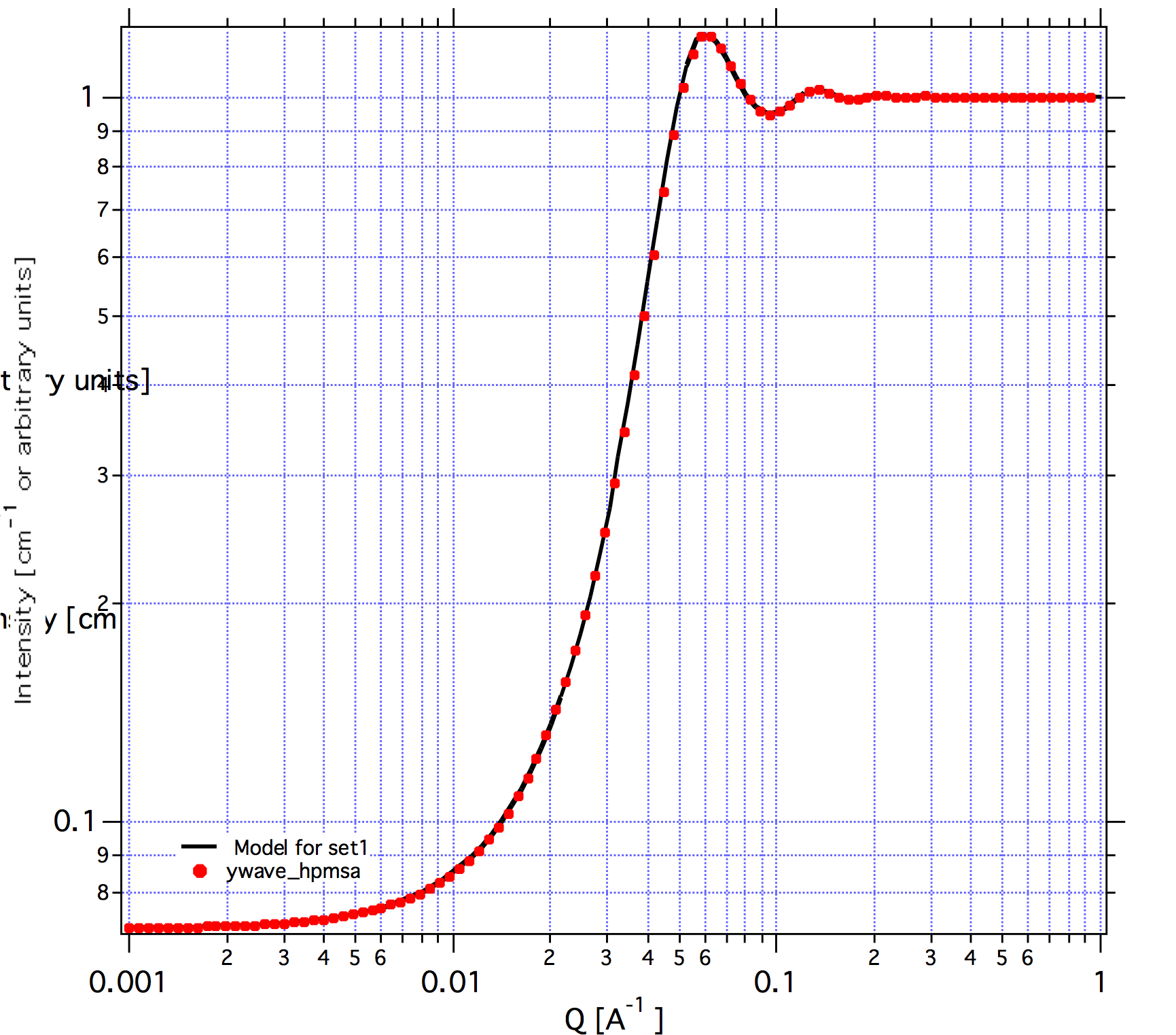
This is graph fro standard NIST set of parameters for both Irena package (black line) and NIST package (red dots). Both assume ONLY structure factor (Form factor is set to 1). The parameters were:
Units are mentioned in the help for each filed on the Structure factor panel (you may have to enable help on Mac, it is shown always on PC in the bottom left corner of the Igor window).
Important note: this is comment from original NIST code.
InterPrecipitate¶
The code for this structure factor has been created on user request for study of precipitation in metals. It is based on formula 6 from APPLIED PHYSICS LETTERS 93, 161904 (2008), Study of nanoprecipitates in a nickel-based superalloy using small-angle neutron scattering and transmission electron microscopy by : E-Wen Huang, Peter K. Liaw, Lionel Porcar, Yun Liu, Yee-Lang Liu, Ji-Jung Kai, and Wei-Ren Chen. This manuscript refers for this formula to paper by R. Giordano, A. Grasso, and J. Teixeira, Phys. Rev. A 43, 6894 (1991). I did not look up original reference, so check it yourself to make sure thef ormula is OKÅc
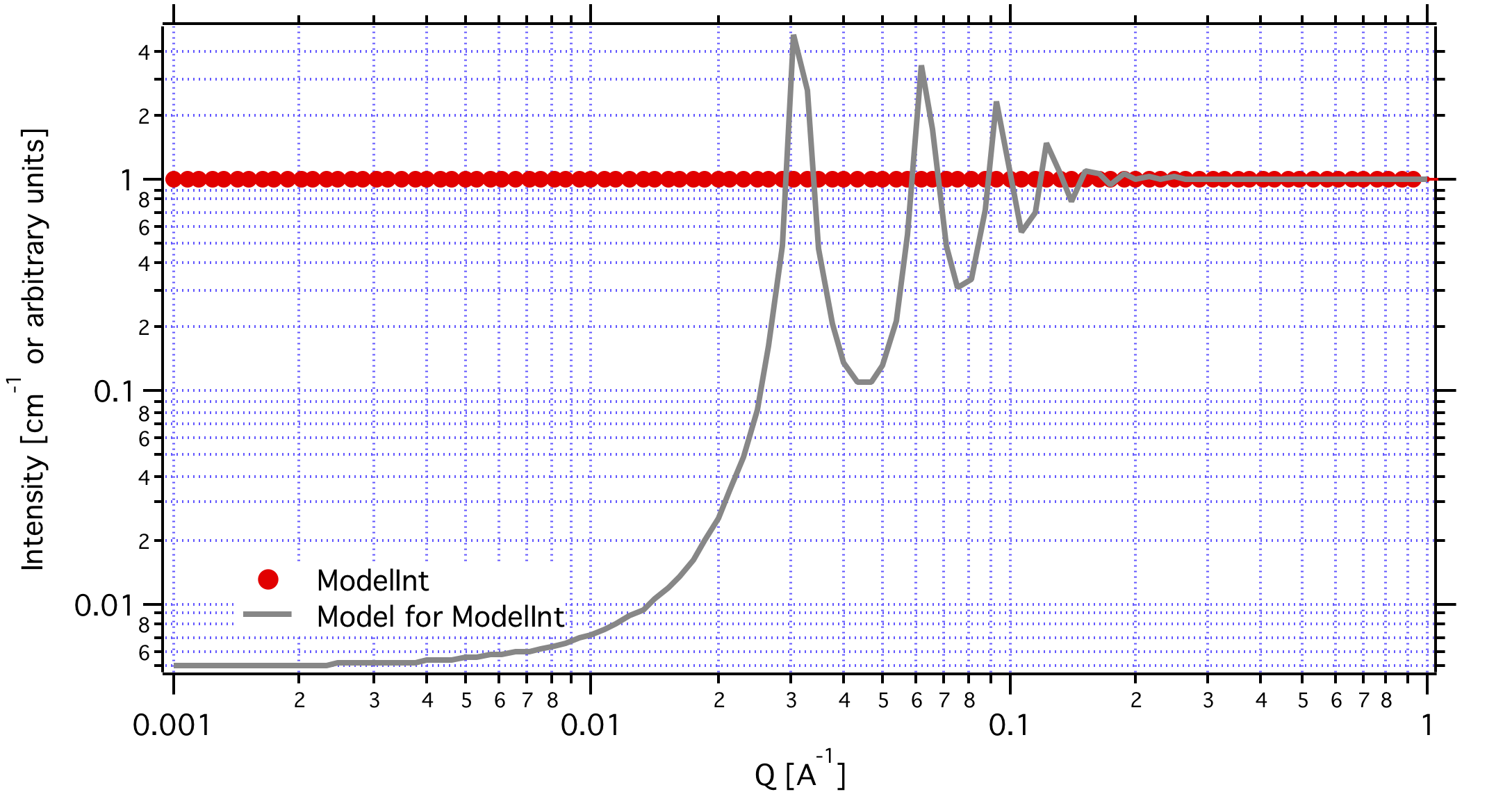
Structure factor has two parameters - L distance and sigma - root-mean-square deviation (ordering factor):
In Igor code this is programmed:
top = \(1 - \exp(-(Q^2\sigma^2)/4)cos(QL)\)
bot = \(1-2\exp(-(Q^2 \sigma^2)/4)cos(QL) + \exp(-(Q^2\sigma^2)/2)\)
\(S(Q,L,\sigma) = 2\frac{top}{bot} - 1\)
This is model of the SF for L=200 and Sigma=20 (Sigma/L=10). I have no way of testing this so this formula has not been checked against any data.
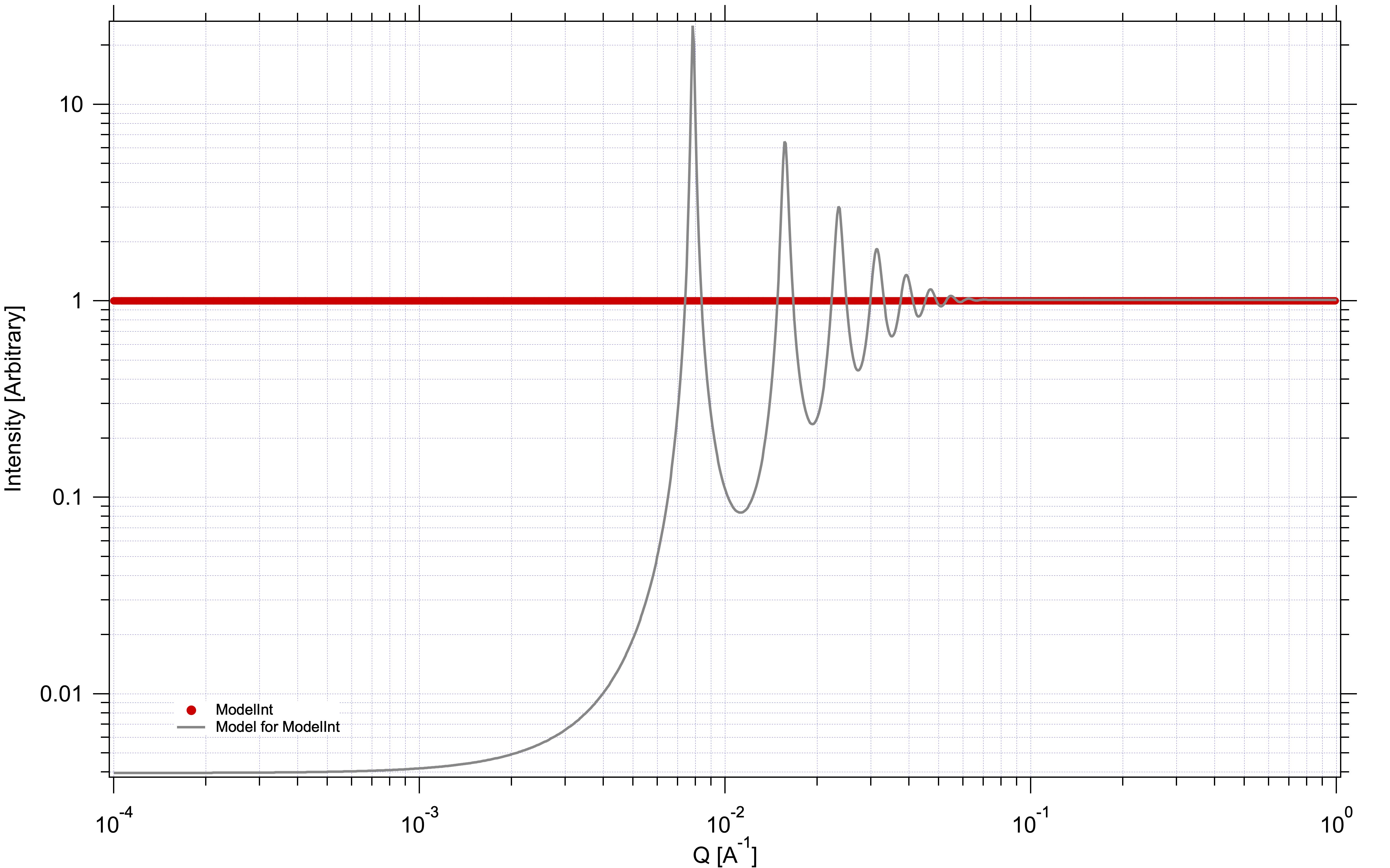
DisorderedCrystal¶
The code for this structure factor has been created on user request. Formula can be found on wikipedia: https://en.wikipedia.org/wiki/Structure_factor#Finite_crystals_with_disorder_of_the_second_kind and is this equation from the web site :
https://wikimedia.org/api/rest_v1/media/math/render/svg/2fcf3e7d435e9a597a2f872ad0df72bd4352bbbd (linked on 8/12/2021)
Structure factor has two parameters - distance “a” and Gausian distribution width = ordering factor \(\sigma\). Formulas are here:
\(r = \exp(-Q^2\sigma^2/2)\)
This is model of the SF for L=800 and Sigma=50. I have no way of testing this so this formula has not been checked against any data.
Calling the library and use¶
Users can use built in library in their own code using following calls:
initialize by calling: IR2S_InitStructureFactors()
this is where the list of known structure factors is: SVAR ListOfStructureFactors=root:Packages:StructureFactorCalc:ListOfStructureFactors
use by calling:
IR2S_CalcStructureFactor(SFname,Qvalue,Par1,Par2,Par3,Par4,Par5,Par6)
I(Q) = I(Q, dilute limit) * IR2S_CalcStructureFactor(SFname,Qvalue,Par1,Par2,Par3,Par4,Par5,Par6)
3. Get panel by calling: IR2S_MakeSFParamPanel(TitleStr,SFStr,P1Str,FitP1Str,LowP1Str,HighP1Str,P2Str,FitP2Str,LowP2Str,HighP2Str,P3Str,FitP3Str,LowP3Str,HighP3Str,P4Str,FitP4Str,LowP4Str,HighP4Str,P5Str,FitP5Str,LowP5Str,HighP5Str, P6Str,FitP6Str,LowP6Str,HighP6Str,SFUserSFformula)
to disallow fitting of parameters, simply set FitP1Str=”” etc. Then you do not have to set low and high limits …
Structure factors package… IR2_OldInterferences this is roughly hard spheres (close to Percus-Yevick model, not exactly), the ETA = 2* radius and Phi = 8 * vol. fraction for PC model. IR2_HardSphereStruct this is Percus-Yevick model IR2_StickyHS_Struct this is sticky hard spheres IR2_SquareWellStruct this is Square well IR2_HayterPenfoldMSA this is HayterPenfoldMSA IR2_InterPrecipitateSF this is InterPrecipitate
Following Form factors have been removed from Irena in version 2.67¶
Unified_Sphere - removed in version 2.67¶
This is formula from Unified fit model by Greg Beaucage (see Unified tool and documentation for it). The parameters are calculated from the code in the manual for each different shape. Specific formulas for these shapes were provided by Dale Schaefer…
- This is the code:
G1=1 P1=4 Rg1=sqrt(3/5)*radius B1=1.62*G1/Rg1^4 QstarVector=qvalue/(erf(qvalue*Rg1/sqrt(6)))^3 F^2 = G1*exp(-qvalue^2*Rg1^2/3)+(B1/QstarVector^P1)
Example for R=50A compared with the spheroid with aspect ratio =1
Unified_Rod - removed in version 2.67¶
Unified_RodAR - removed in version 2.67¶
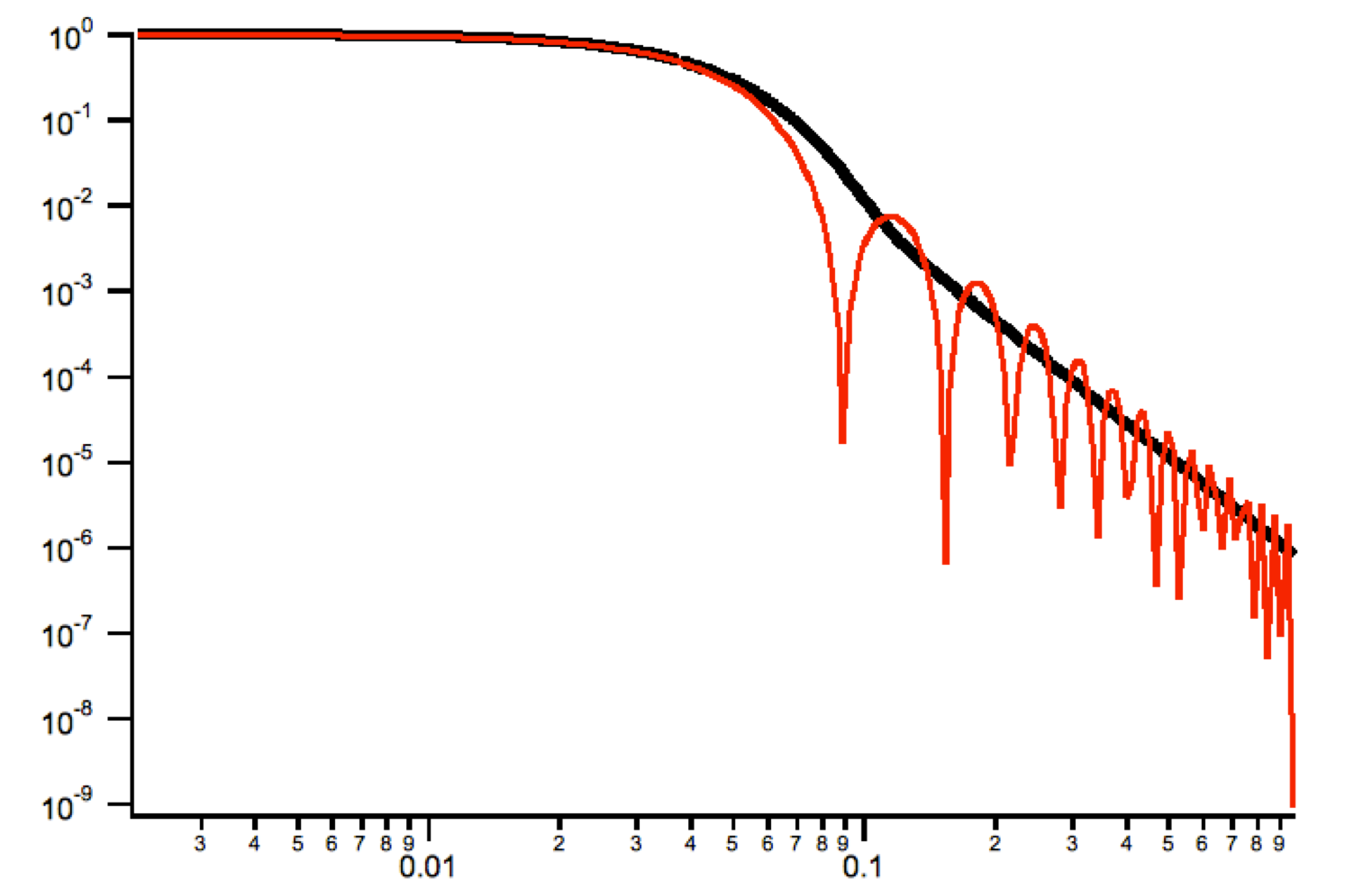
This is formula from Unified fit model by Greg Beaucage (see Unified tool and documentation for it). The parameters are calculated from the code in the manual for each different shape. Specific formulas for these shapes were provided by Dale Schaefer…
- This is the code:
G2 =1 Rg2=sqrt(Radius^2/2+Length^2/12) B2=G2*pi/length P2=1 Rg1=sqrt(3)*Radius/2 RgCO2=Rg1 G1=2*G2*Radius/(3*Length) B1=4*G2*(Length+Radius)/(Radius^3*Length^2) P1=4 QstarVector=qvalue/(erf(qvalue*Rg2/sqrt(6)))^3 A=G2*exp(-qvalue^2*Rg2^2/3)+(B2/QstarVector^P2) * exp(-RGCO2^2 * qvalue^2/3) QstarVector=qvalue/(erf(qvalue*Rg1/sqrt(6)))^3 F^2 = A + G1*exp(-qvalue^2*Rg1^2/3)+(B1/QstarVector^P1)
Example for R=50A and length 500A compared with the cylinder
Unified_Disk - removed in version 2.67¶
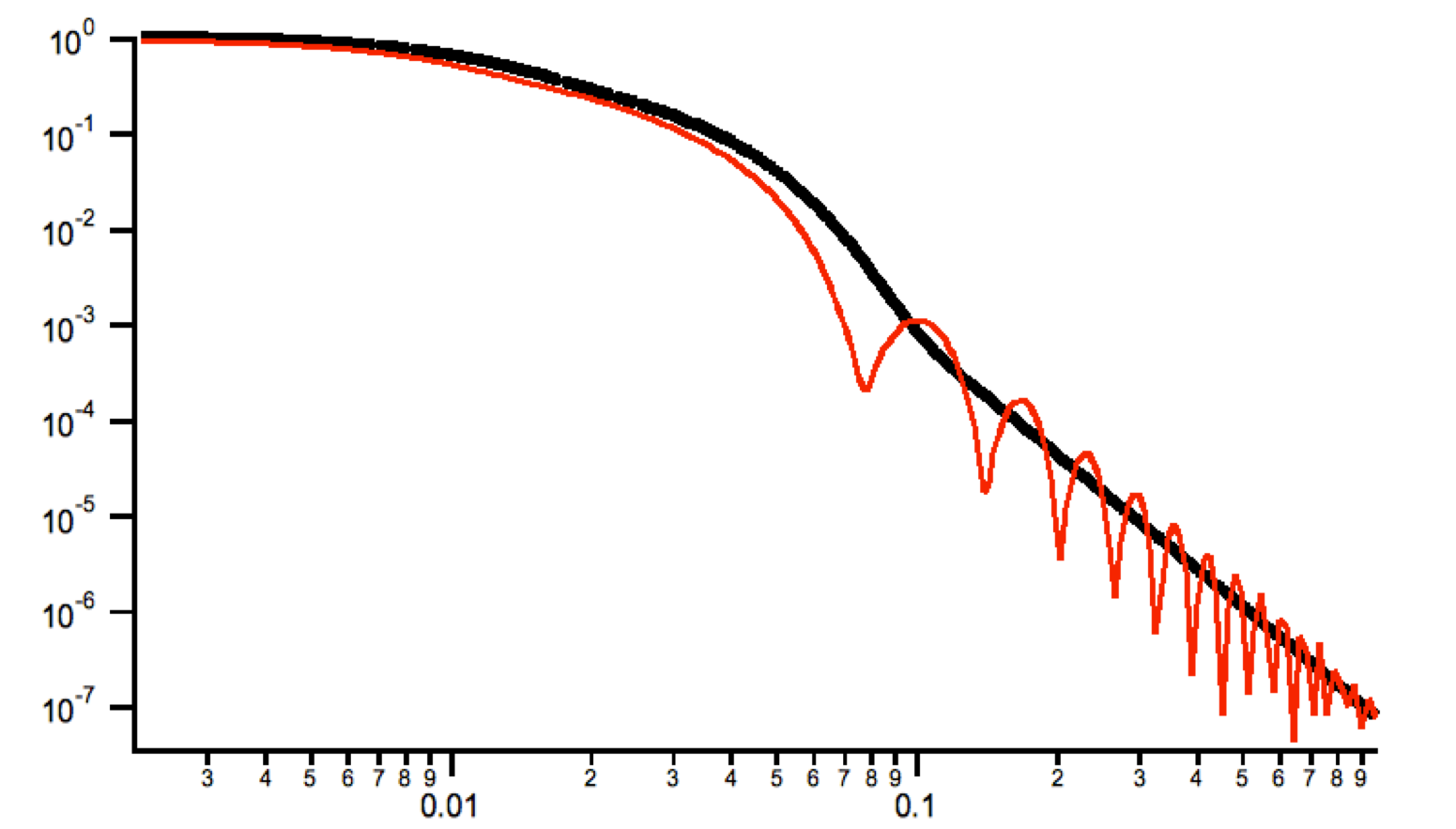
This is formula from Unified fit model by Greg Beaucage (see Unified tool and documentation for it). The parameters are calculated from the code in the manual for each different shape. Specific formulas for these shapes were provided by Dale Schaefer…
- This is the code:
G2=1 Rg2=sqrt(Radius^2/2+thickness^2/12) B2=G2*2/(radius^2)//dws guess P2=2 Rg1=sqrt(3)*thickness/2// Kratky and glatter = Thickness/2 RgCO2=1.1*Rg1 G1=2*G2*thickness^2/(3*radius^2) B1=4*G2*(thickness+Radius)/(Radius^3*thickness^2)//same as rod P1=4 QstarVector=Q/(erf(Q*Rg2/sqrt(6)))^3 A=G2*exp(-Q^2*Rg2^2/3)+(B2/QstarVector^P2) * exp(-RGCO2^2 * Q^2/3) QstarVector=Q/(erf(Q*Rg1/sqrt(6)))^3 F^2 = A + G1*exp(-Q^2*Rg1^2/3)+(B1/QstarVector^P1)
Example for R=250A and thickness 10A compared with the cylinder