System specific models¶
This tool provides GUI for models which are basically analytical formulas applicable to specific microstructures: Debye-Bueche, Treubner-Strey, Ciccariello-Benedetti, Hermans, Modified Hermans, and Unified Green Born model
Debye-Bueche model for modeling structural in homogeneities in the gels. https://onlinelibrary.wiley.com/iucr/itc/Ha/ch5o8v0001/sec5o8o3o1o4/
Treubner-Strey model for modeling of small-angle diffraction
Ciccariello-Benedetti for coated smooth surfaces
Hermans, Modified Hermans, and Unified Green Born all of these are for polymers with lamellar structures. For details see: https://doi.org/10.1016/j.polymer.2021.124281
Most models can be combined with low-Q Single Unified level. New generation GUI enables ONLY one model be applied to any data at time.
For explanation of the Unified level control, please see Unified fit. Unified can have RgCo linked to best guess combination of parameters from Debye-Bueche, Treubner-Strey, and some other models. Residuals are plotted as dots in the graph.
Tool overview and use¶
The use of the tool will be demonstrated on Debye-Bueche model, but is similar for all models. The tool uses new generation data selection tool, used by Muti Sample Plotting tool, all bioSAXS tools, etc. see. In the top part are controls which allow users to choose what data will be listed in the listbox. Choices are USAXS data or QRS data, USAXS can be slit smeared or desmeared and one can use “Folder match string” (uses Regular expressions, see bottom of panel for hints how to use them).
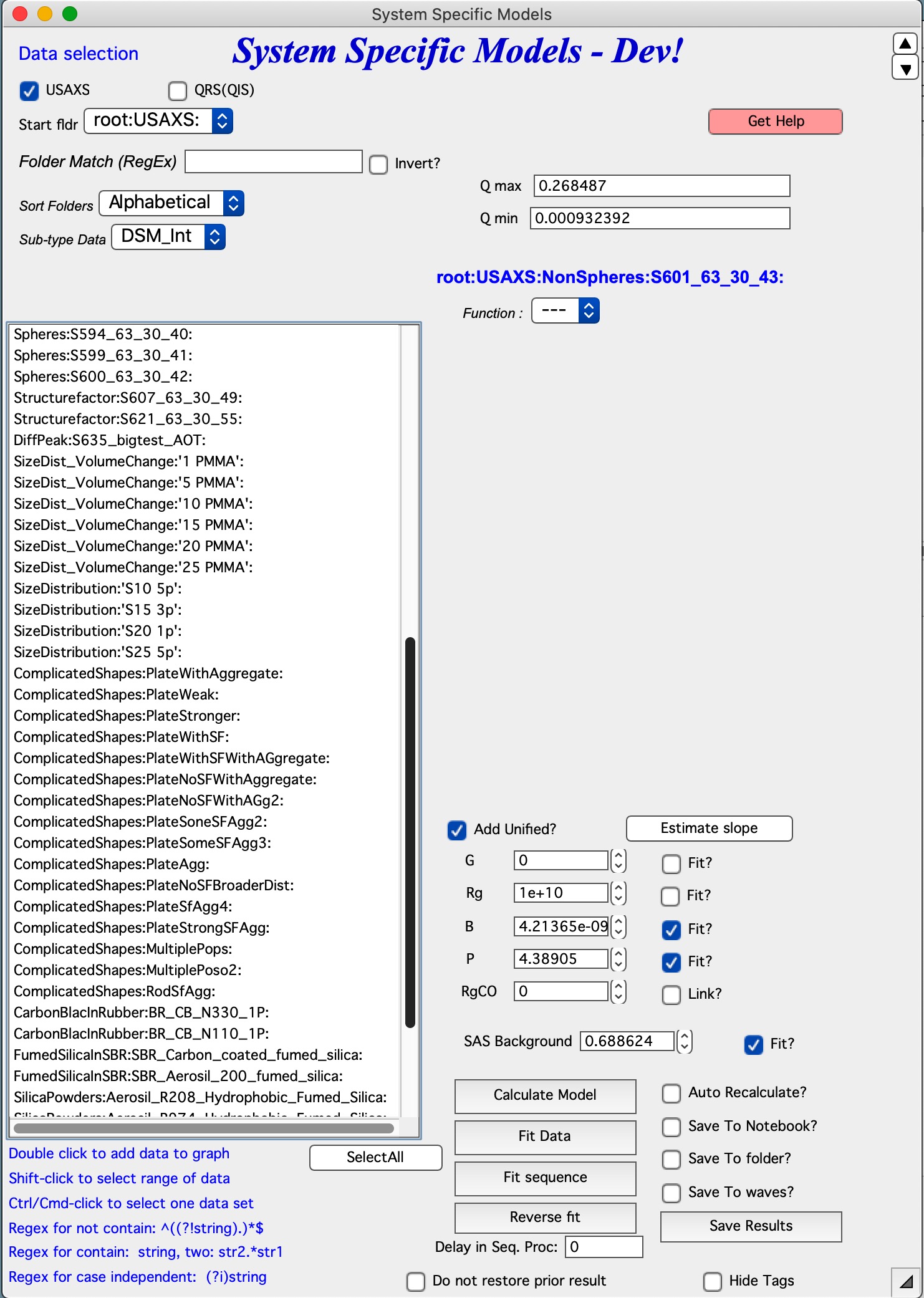
Controls¶
Pick data type of the top to display dat you want to see and order them the way you need. Add one data set into the tool by double click a dataset. This will add the data in the tool and create a log-log plot. The blue letters above the Model pulldown menu show, which data set is currently being analyzed.
Model
Pick model from pull down menu. Area under the pulldown menu will be populated with controls appropriate for that specific model. Details will be discussed in model sections below.
Unified fit
Unified fit controls are below the Model area. Use checkbox “Add Unified?” to display them and add Unified level scattering to the model. There are 5 parameters - G, Rg, P, and B - and RgCO parameter, which can be linked to best guess combination of parameters of specific models. This RgCO is critically important parameter to understand - if used, scattering from Unified level is terminated at RgCO size and in simplistic term this means, that scattering of the Unified fit level is coming from material which scatters also at smaller sizes.Effectively this states, that Unified fit level and model scattering come from the same phase (material). If Unified fit level would be scattering of different phase (e.g., surface scratches on the sample), RgCO would be 0 and would not be linked to anything. In this case scattering from Model and Unified fit level are independent and total sample scattering is simple sum at each Q. Button Estimate slope withs P and B to range fo data selected by cursors.
Background
Background is assumed simply flat background, same for all Q values. Can be set by user and fitted if appropriate.
Calculate & Save buttons/controls
These buttons and checkboxes control, how the data are fitted and results saved.
Calculate model Calculates model with current values of parameters. “Auto Recalculate?” checkbox will force Calculate model after every parameter change. Useful when enough cpu is available.
Fit data fits data, current data set in the tool, fits only parameters which have “Fit?” checkbox selected. Pay attention to data ranges. TODO: at this time no warning is provided to users when parameter fitting range is reached.
Fit sequence button - fits sequence of data selected in the Listbox with data sets. Fits data from top to bottom, so if needed, user should make sure samples are sorted in proper order. Note, that
Revert fit button – use to reset the last set of parameters after bad fit which “lost it’s way”…
Save results button - will save model data for further use. What exactly is saved depends on checkboxes above. See description below.
Auto recalculate? checkbox - forces recalculation when any parameter is changed.
Save to Nogtebook? checkbox - appends summary of results and plot to the end of results notebook. Useful when you want to export summary of results. Human readable - and you can edit notebook, so it is useful as tool for making notes.
Save to folder checkbox - this will save waves with results (Q, and intensity) into data folder. They can be plotted later and also can be “recovered” - if same solution has been found in the folder, code will offer to reload the parameters from this solution. Useful when you need to jump through many data sets.
Save to waves checkbox - creates folder (e.g. for Debye-Bueche root:DebyeBuecheResults: ) and save waves with each individual parameter there. Data are added in order they are processed, wave with folder names is also created. This is useful when you need easy way of plotting the results of sequence of analysis.
Delay in Seq. Proc: sets time which code waits in between analysis of data sets in sequence. Useful for visual inspection and making notes when processing larger set of data.
Do not restore prior results checkbox - if checked, code will not offer to restore prior results, if found.
Hide tags checkbox - will hide tags with results which can get pretty annoying. If checked, tags will be removed. Uncheck, tags are always added.
**********************************
Models details¶
Debye-Bueche model for gels¶
The theory (https://onlinelibrary.wiley.com/iucr/itc/Ha/ch5o8v0001/sec5o8o3o1o4/) is implemented in following form:
where \(K = 8 \pi ^2 \lambda^{-4}\)
Parameters of the gel are then the corrL – correlation length and \(\varepsilon\). The model also allows low-q power law to be fitted and subtracted from data as well as flat SAS background. The low-q power law slope has 2 parameters (slope and prefactor) and background has one. All can be fitted.
Following citation from Hammouda, NIST, web presentation: The Debye-Bueche model is used to describe scattering from phase-separated (two- phase) systems. Here also correlations are characterized by an e-folding length ξ. The pair correlation function is give by (Debye-Bueche, 1949):
The scattering cross section is obtained by taking the Fourier transform to obtain:
The prefactor can be expressed in terms of the volume fraction φ and contrast factor \(\Delta \rho^2\) as:
The Debye-Bueche model is obtained as a special case of the Teubner-Strey model for
very large d-spacing (d>>ξ).
This is the typical plot:
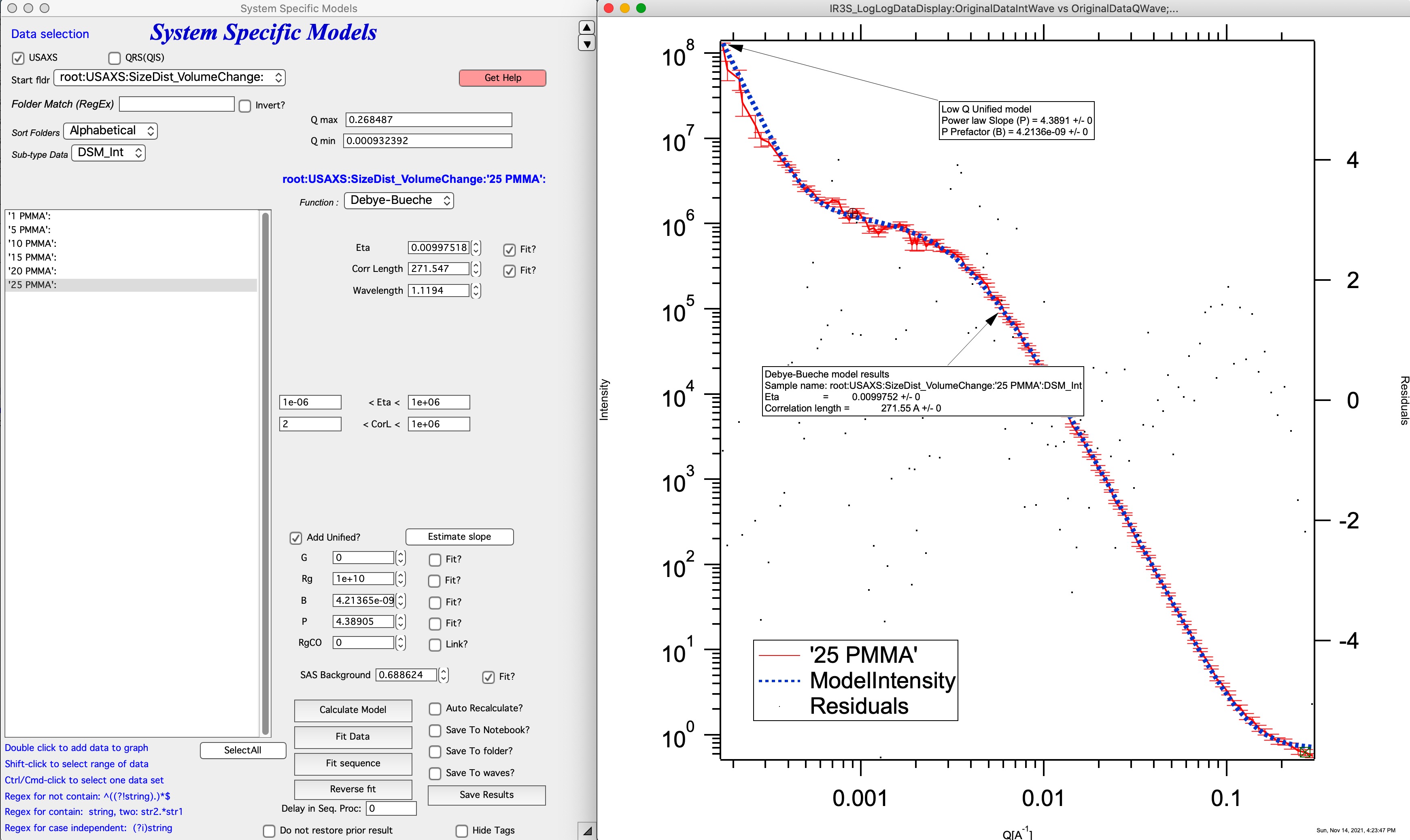
In this plot we use Eta and Corr length, wavelentgth is read from header or can be set by user, if needed. We also use Power law slope part of Unified fit (see Unified fit for details and why is G=0 and Rg=10^10).
*************************************
Treubner-Strey for small-angle diffraction¶
Treubner-Strey model follows the publications : Teubner, M; Strey, R. J. Chem. Phys., 1987, 87, 3195 (https://doi.org/10.1063/1.453006) and Schubert, K-V.; Strey, R.; Kline, S. R. and E. W. Kaler J. Chem. Phys., 1994, 101, 5343 (https://doi.org/10.1063/1.467387). More current description also in: https://doi.org/10.1016/j.polymer.2004.08.033
The code is adopted form NIST SANS package. The formulas are:
Where A, C1 and C2 are parameters from the theory and TS is scaling factor.
Correlation length °ξ and repeat distance (d) are:
Example of the GUI with results:
Note, that only the parameters TS, A, C1, and C2 are user controlled. Parameter TS is added scaling factor, as there does not seem to be other way to scale the model to data.
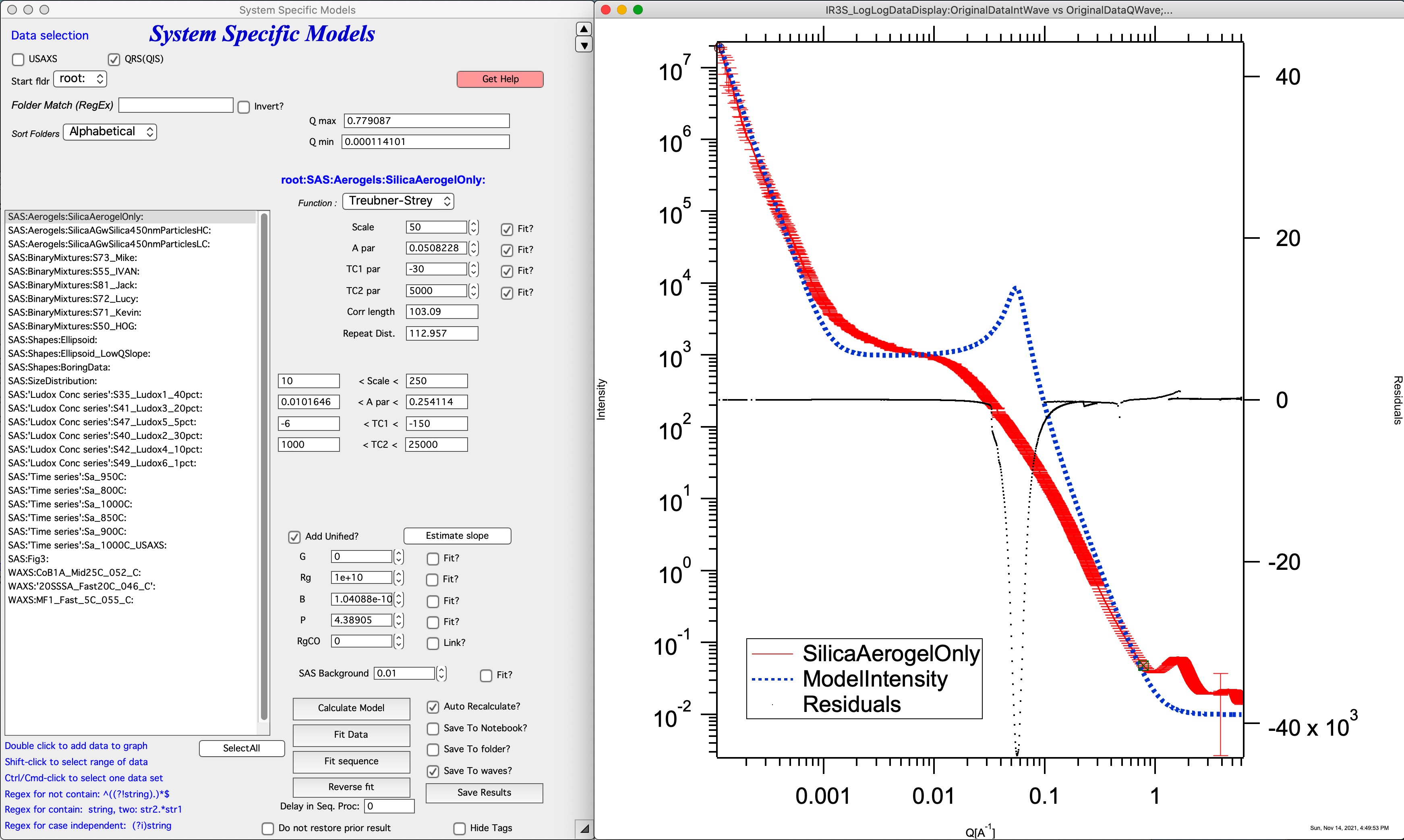
This is example of plot of Treubner-Strey model on arbitrary data, I do not seem to have handy original data from ~2005 when this was coded and tested.
*************************************
Ciccariello–Benedetti model for coated smooth surfaces¶
This tools was coded using following manuscripts:
Benedetti, A., S. Ciccariello, Coated Silicas and Small-angle X-ray intensity behavior, J. Appl. Cryst (1994) 27, 249-256.
Pikus, S., E. Kobylas, and S. Ciccariello, Small-angle scattering characterization of n-aliphatic alcohol films adsorbed on hydroxylated porous silicas, J. Appl. Cryst. (2003) 36, 744-748,(https://doi.org/10.1107/S0021889803000244).
And tested on experimental data provided by S. Ciccariello. Note, that the experimental data were only slit smeared and that I have found some interesting discrepancies between using finite slit length (and using internal smearing routines of Irena for slit smearing the model) and running provided specific code for slit smeared data (assuming infinite slit length). Simply put, the results vary depending on slit length and one needs to be careful on this. Please, read further…
In summary, this model assumes that on surfaces of porous media is present constant thickness and constant scattering length density layer. The surface of the film is assume to be always parallel with the surface of the solid. Basically, it is coated porous surface with very specific layer – since this is modification of Porod’s law, it is clear that the interfaces must be sharp. In this case the Porod’s Q-4 power law is modified by oscillatory behavior from which one can extract the thickness and scattering contrast of the film. For more details, please read the manuscripts.
Ciccariello-benedetti example:
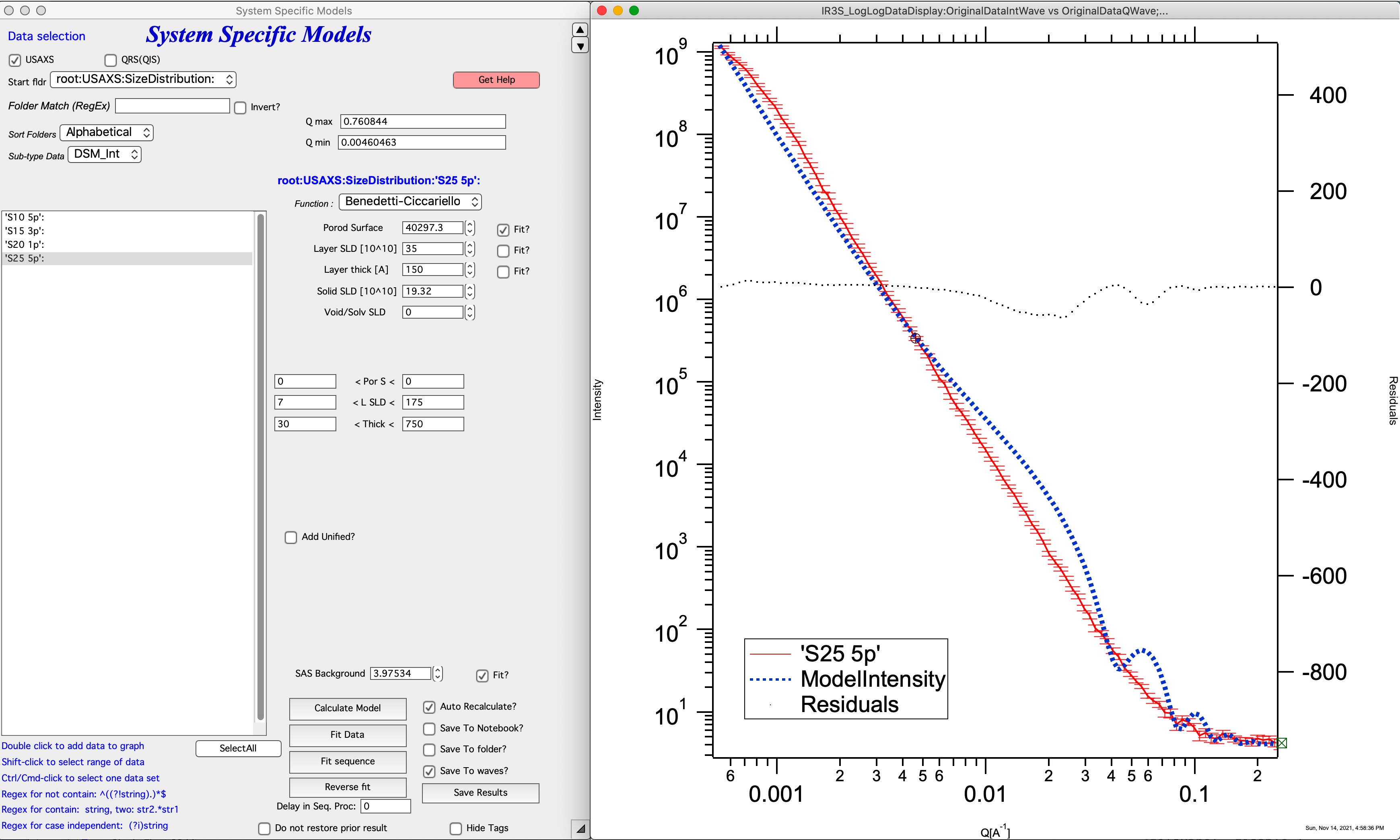
The model has three main parameters, which can be fitted:
Porod specific surface area (area of the solid/void or solid/solvent) interface. This is area of the interface without the layer on.
Layer rho - scattering length density of the layer material
Layer thickness - thickness of layerin [A]
And the model has two parameters which area assumed to be known:
Scattering length density of the solid (rho) and scattering length density of the void/solvent (material which is inside the voids). If this is air, it is likely 0.
Note, that one may need to select also SAS background and set fitting limits and “Fit?” checkboxes as in other tools. Alos, this is one model where combination with Unified fit makes little sense, usually…
*************************************
Hermans model for lamellar systems¶
The Hermans model assumes independent, normal distributions for the crystalline and amorphous regions of lamellae. It also assumes the lamellae are composed of infinitely wide, perfectly aligned, and regularly spaced sheets. Details about lamellae imperfections cannot be obtained from the fit. The model directly fits the scattered intensity from SAXS and USAXS measurements. Five independent parameters are used to determine the long period which include the mean crystalline thickness (tL), the standard deviation of the crystalline thickness (σL), the mean amorphous thickness (ta), the standard deviation of the amorphous thickness (σa), and a Porod prefactor for surface scattering (B1). While it can be extended to USAXS measurements, since the model assumes perfectly lamellar sheets it leads to a -2 power law slope at low-q measurements. The Hermans model describes the surface scattering Porod region at high-q, the Guinier region for the lamellar thickness, the structure factor for stacking of lamellae, and the two-dimensional scaling regime for infinite width lamellae. The function does not describe the lateral extent of the lamellae or higher order structures such as fibrous stacks and meso-structures such as spherulites.
For details see: https://doi.org/10.1016/j.polymer.2021.124281
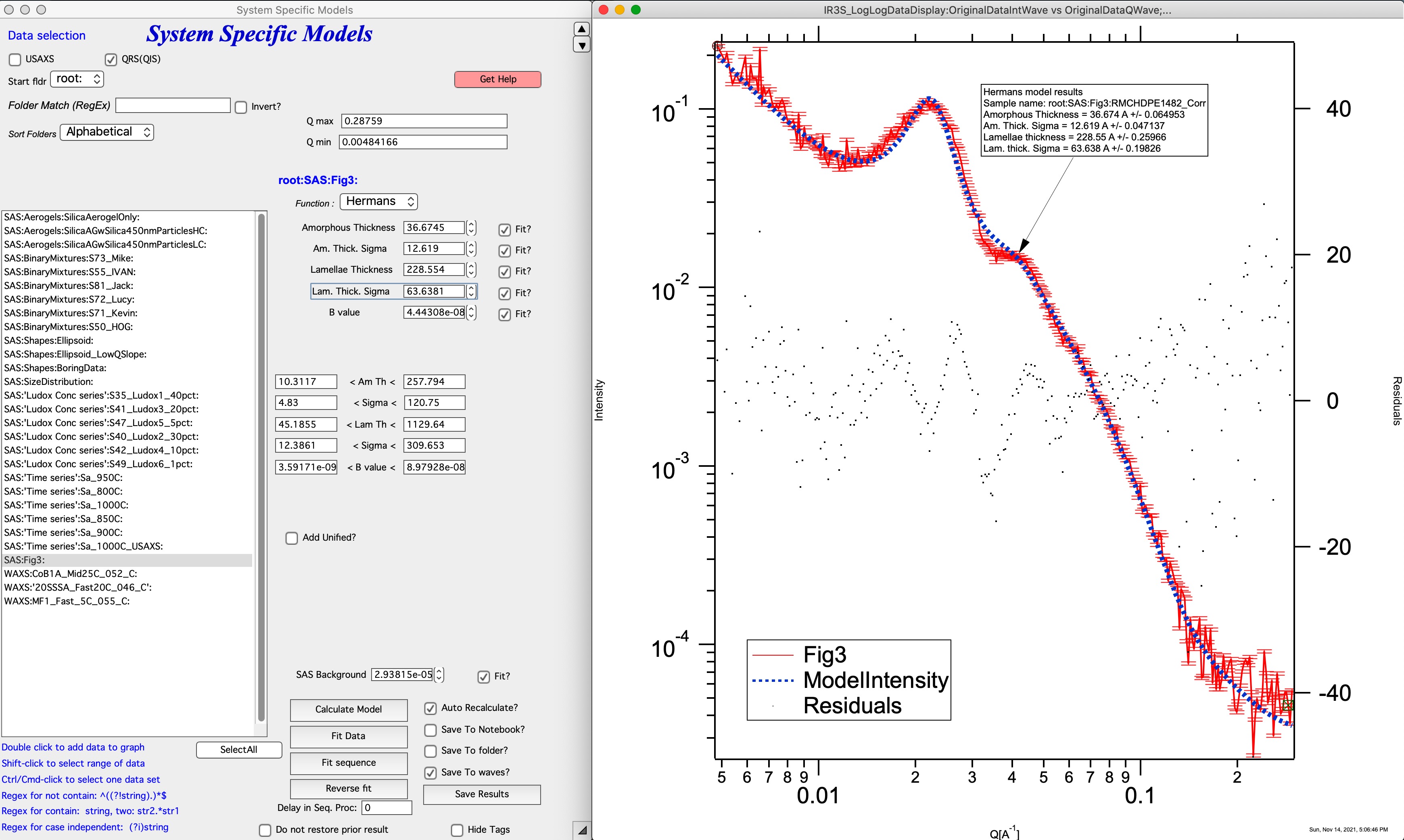
Comment: this model has many parameters, it is questionable how many unique solutions are there.
*************************************
Modified Hermans model for lamellar systems¶
Like the Hermans model, the hybrid-Hermans model assumes independent, normally distributed crystalline and amorphous thicknesses of lamellae sheets and these lamellar sheets are composed of perfectly aligned, infinitely wide, and regularly spaced. The hybrid-Hermans model also describes the surface scattering Porod region at high-q, the Guinier region for the lamellar thickness, and the structure factor for stacking of lamellae. However, this function adds additional terms from the Unified function1 to describe the higher order structures associated with the lamellae stacks. The hybrid-Hermans model has the same parameters as the Hermans model to describe the lamellae but requires two extra parameters (Rg,2 and G2) for a total of seven parameters when limited to the lamellar width.
For details see: https://doi.org/10.1016/j.polymer.2021.124281
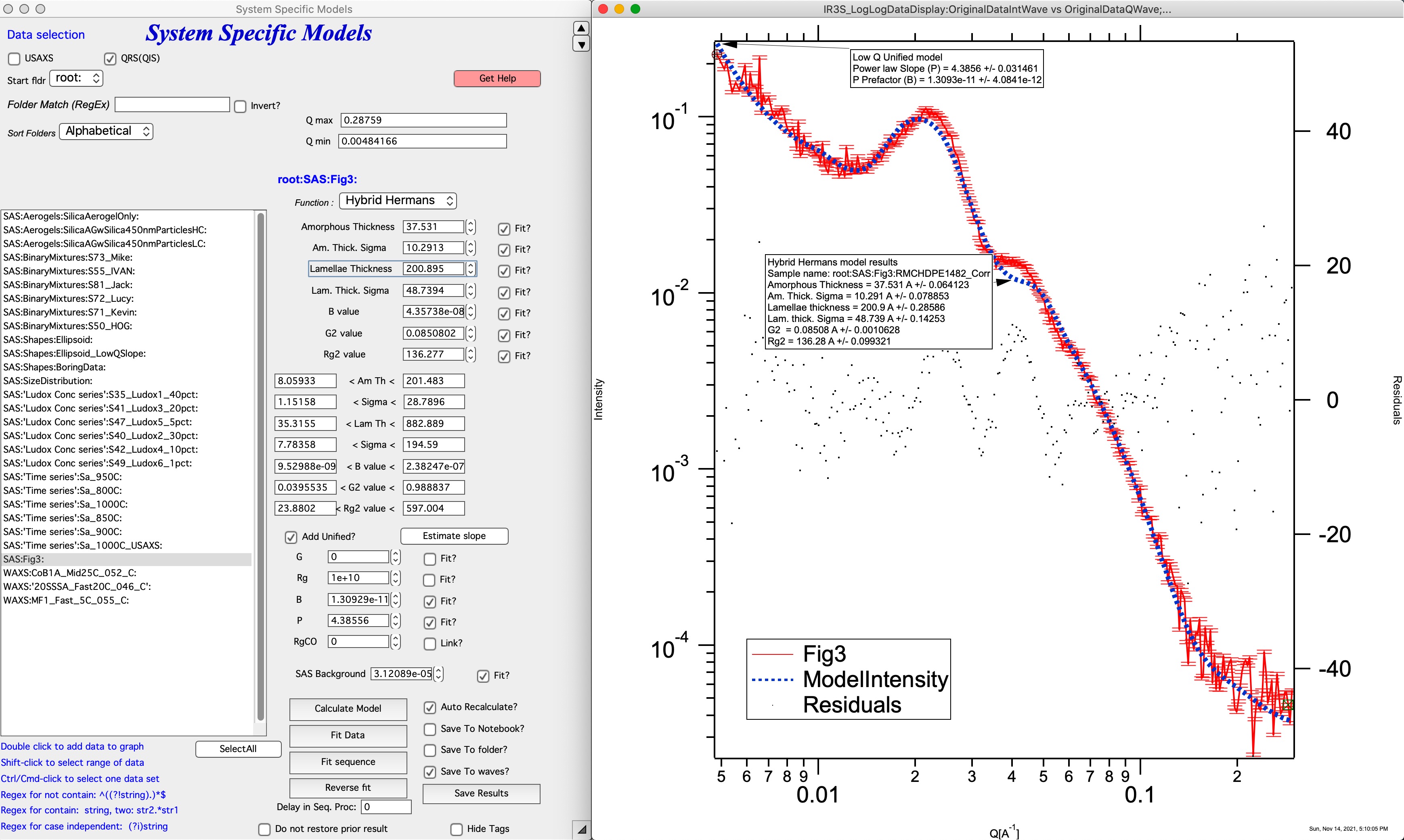
Comment: this model has many parameters, it is questionable how many unique solutions are there. *************************************
Unified Born Green model for lamellar systems¶
The Unified Born-Green model assumes that the lamellae are laterally symmetric, have a platelet structure, and the only contrast present is between the amorphous and crystalline regions. In contrast to the Hermans and hybrid-Hermans models, the Unified Born-Green model also assumes two-dimensional correlations between the lamellae stacks (i.e. thickness and lateral directions). The model requires 6 parameters (Rg,1, B1, p, ξ, δ, kI) to describe the lamellar features. The Unified Born-Green function can be modified to include additional parameters to describe higher order lamellar structures.
For details see: https://doi.org/10.1016/j.polymer.2021.124281
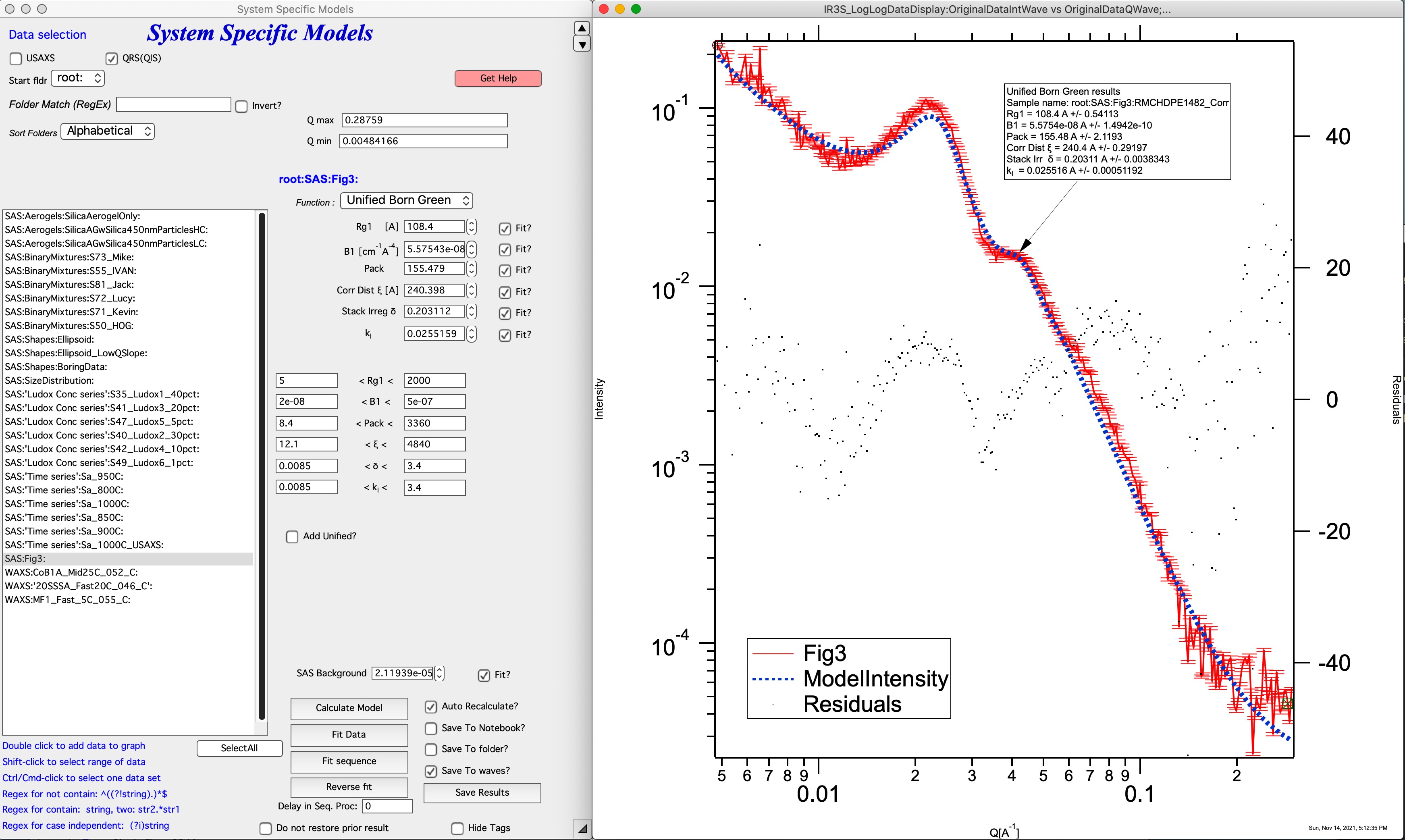
Comment: this model has many parameters, it is questionable how many unique solutions are there.